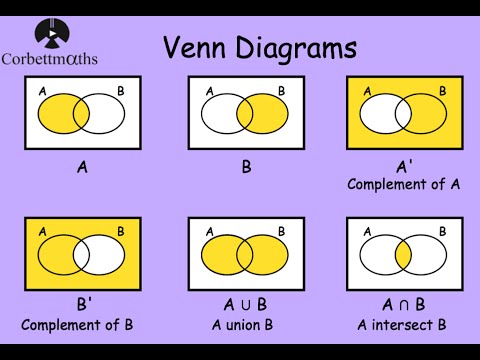
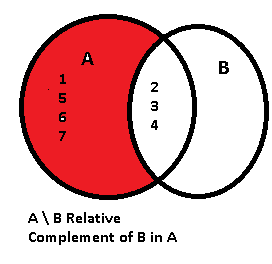
In set theory, the complement of a set A refers to elements not in A. When all sets under consideration are considered to be subsets of a given set U, the absolute complement of A is the set of elements in U but not in A. The relative complement of A with respect to a set B, also termed the If the set A is the suit of spades, then the complement of A is the union of the.
Note: A ∪ A = U, the union of a set with its complement gives the universal set. .
We begin by constructing a Venn diagram, we will use B for the Big Game and. Enter an expression like (A Union B) Intersect (Complement C) to describe a combination of two or three sets and get the notation and Venn diagram.
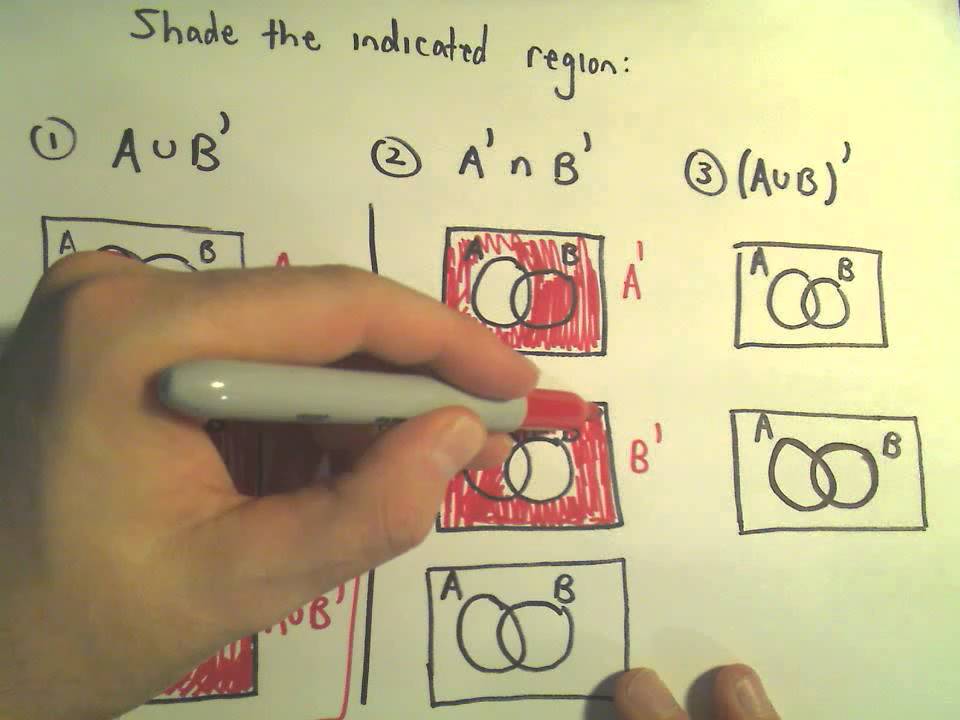
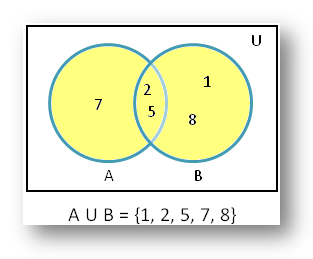
Here we are going to see how to draw a venn diagram for A union B whole complement. Venn diagram of (A U B)’: To represent (A U B)’ in venn diagram, we. Use Venn diagrams to illustrate data in a logical way which will enable you to see We can also find the union of A and B which is written as A ∪ B.
This means we can use the notation A’ called the complement of A. In the example above.Here are some useful rules and definitions for working with sets.
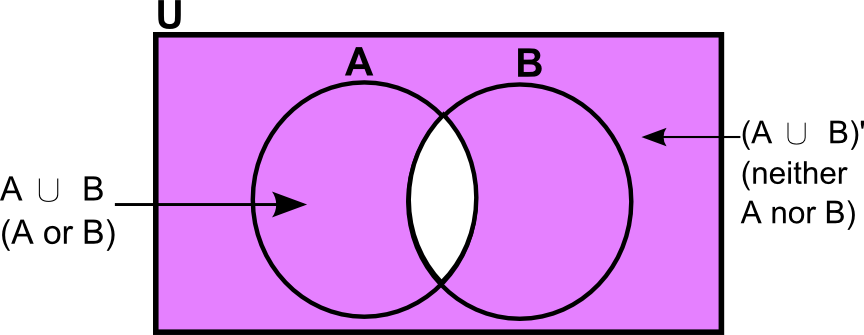
The Venn diagram above illustrates the set notation and the logic of the answer. Since “union” means “everything in either of the sets”, all of each circle is shaded in. (If you’re not clear on the logic of the set notation, review set notation before proceeding further.).
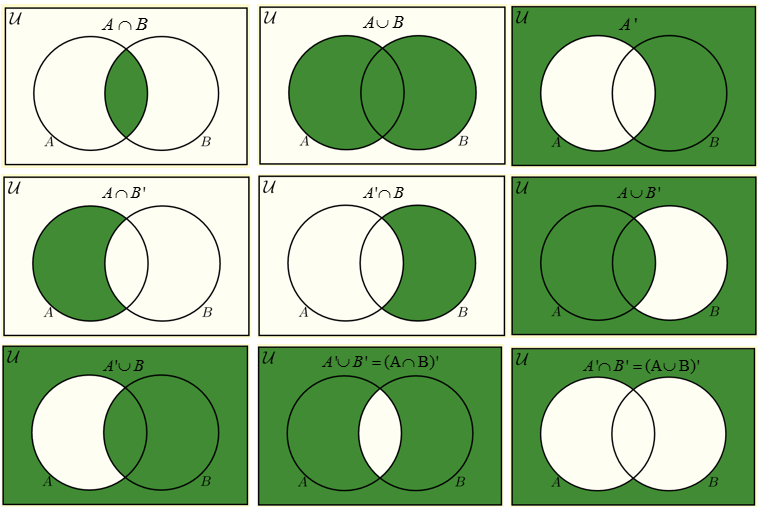
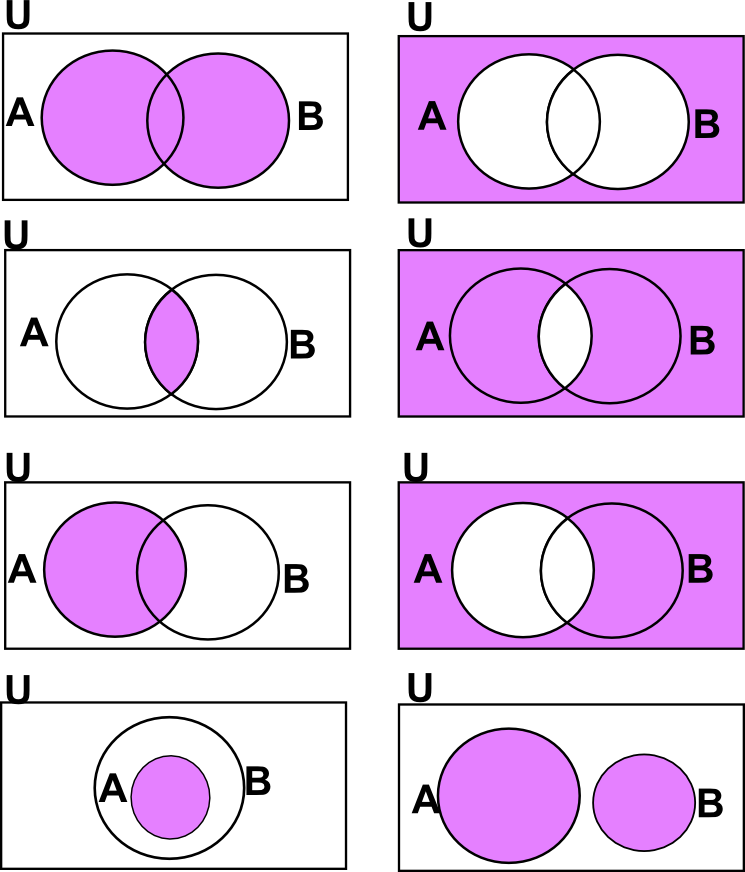
The complement of a set A is everything that is not in A; it is represented by the magenta region in the Venn diagram below (hence the set A is represented by the white region). The union of A and B is everything which is in either A or B, as represented by the magenta shaded region in the following venn diagram.
The complement of a set using Venn diagram is a subset of U. Let U be the universal set and let A be a set such that A ⊂ U. Then, the complement of A with respect to U is denoted by A’ or A\(^{C}\) or U – A or ~ A and is defined the set of all those elements of U which are not in A.
The complement of a set using Venn diagram is a subset of U. Let U be the universal set and let A be a set such that A ⊂ U. Then, the complement of A with respect to U is denoted by A’ or A\(^{C}\) or U – A or ~ A and is defined the set of all those elements of U which are not in A.De Morgans Law – Proof with Examples – Set Theory – TeachooComplement of a Set using Venn Diagram | Example on Complement of a Set