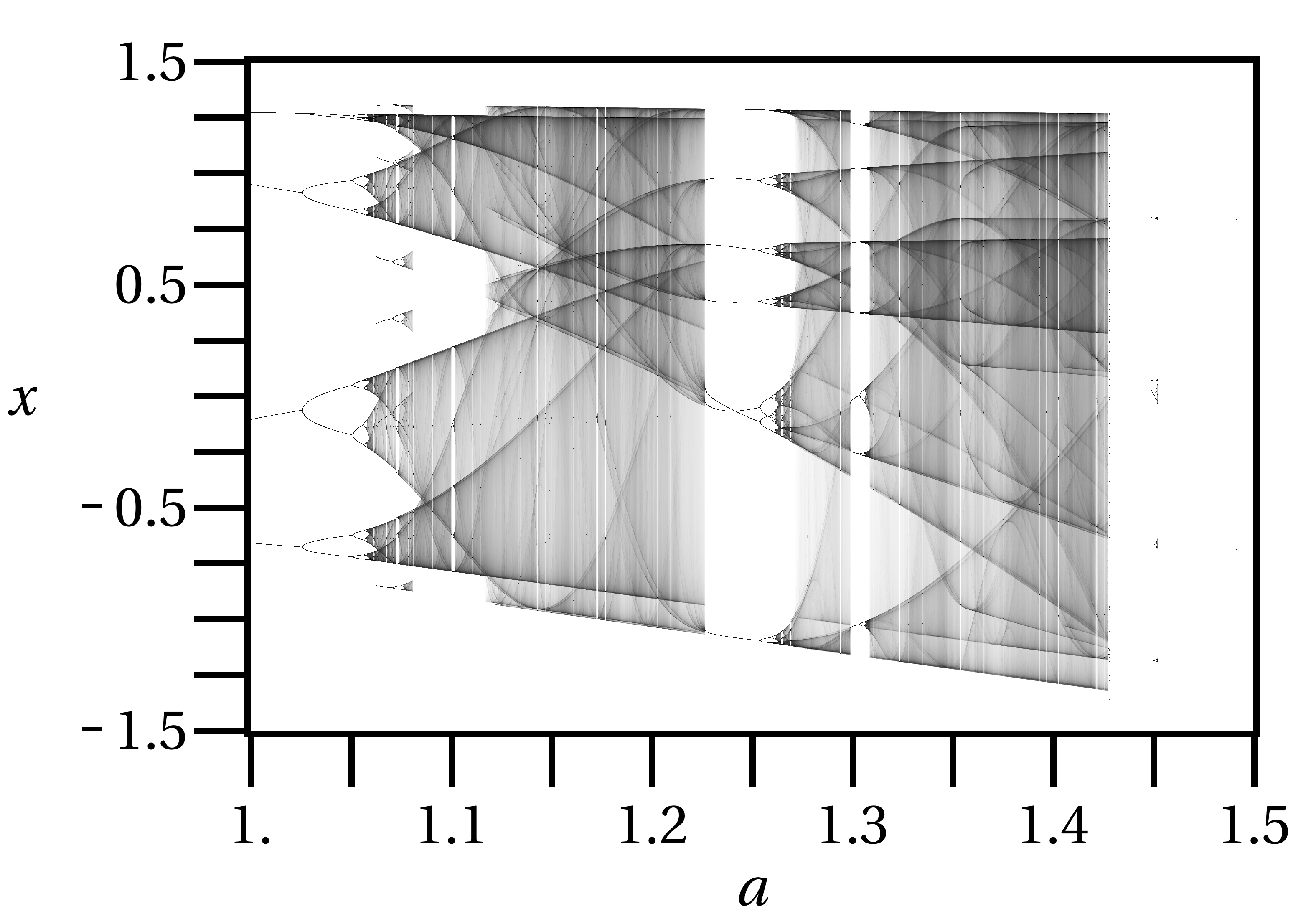
I want to produce a bifurcation diagram using mathematica to represent equilibrium points of p1 using the data obtained from the following code.
Also Mathematica is a useful tool where it is available. See http://mathematica.
schematron.org Feigenbaum’s Scaling Relation for Superstable Parameter Values: Bifurcation Diagrams with Flow Fields, Bifurcation Diagram for a Generalized Logistic Map. q[u_]:= (2 u^3)/(u^2 – 1) r[u_]:= (2 u^3)/(1 + u^2)^2 Show[ParametricPlot[{q[u], r[u ]}, {u, 0, 30}, AspectRatio -> 1/GoldenRatio, PlotRange -> {{4, 30}, {, }}.
Also Mathematica is a useful tool where it is available. See http://mathematica. schematron.orgBifurcation. In a dynamical system, a bifurcation is a period doubling, quadrupling, etc., that accompanies the onset of schematron.org represents the sudden appearance of a qualitatively different solution for a nonlinear system as some parameter is varied.
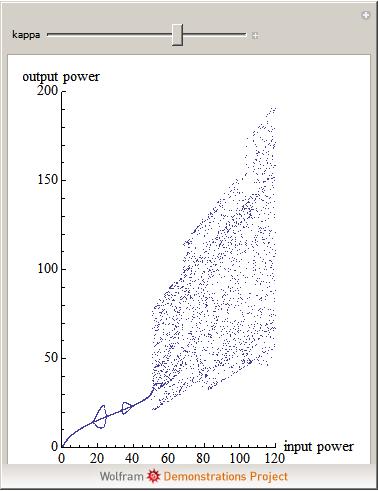
Sep 22, · I want to produce a bifurcation diagram using mathematica to represent equilibrium points of p1 using the data obtained from the following code, . The Demonstration plots the bifurcation diagram, where is the bifurcation parameter, for values of parameters and set by the user. The bifurcation diagram shows the onset of chaotic behavior, period doubling, and so on.
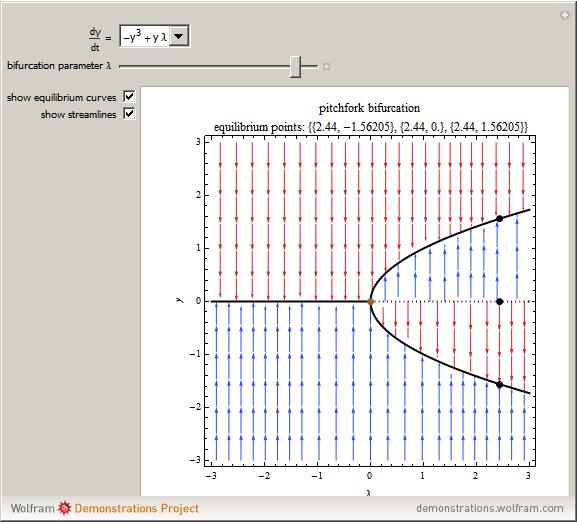
For a dynamical system, bifurcation points are those equilibrium points at which the Jacobian is singular. This Demonstration shows the bifurcation diagrams of several normal form bifurcations in one dimension. The bifurcation point, equilibrium points, and the flow of the vector field are visualized.
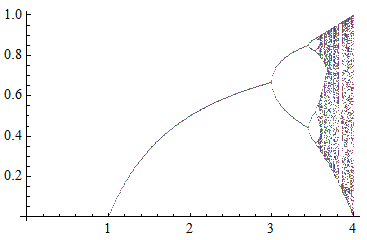
The bifurcation is shown as a brown point. Note that the diagram becomes progressively more complex as τ is increased, and the run time increases correspondingly. Addendum The bifurcations can be seen even more clearly from a return map, for instance.plotting – The right plot to use for bifurcation diagram – Mathematica Stack Exchangedifferential equations – Plotting a Bifurcation diagram – Mathematica Stack Exchange