Students explore fraction equivalence through the decomposition of non-unit and unit fractions.
Students decompose fractions using tape diagrams to represent. Decompose fractions as a sum of unit fractions using tape diagrams. Engage NY’s files Mathematics Grade 4 Module 5 · Download.
Thumbnails Document. decomposition of a fraction early in the module allows students to become fractions in word problems using tape diagrams.

As an extension of the Grade 4. how to decompose fractions as a sum of unit fractions using tape diagrams, Draw a number bond and write the number sentence to match each tape diagram. how to decompose fractions as a sum of unit fractions using tape diagrams, Common Core Grade 4.Mar 08, · This feature is not available right now.
Please try again later. Lesson 1: Decompose fractions as a sum of unit fractions using tape diagrams. 19 This work is derived from Eureka Math ™ and licensed by Great Minds.

©Great Minds. eureka schematron.org This file derived from G4-M5-TE This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike Unported License. Students decompose mixed numbers using tape diagrams to represent them as sums of fractions with the same denominator in different ways.
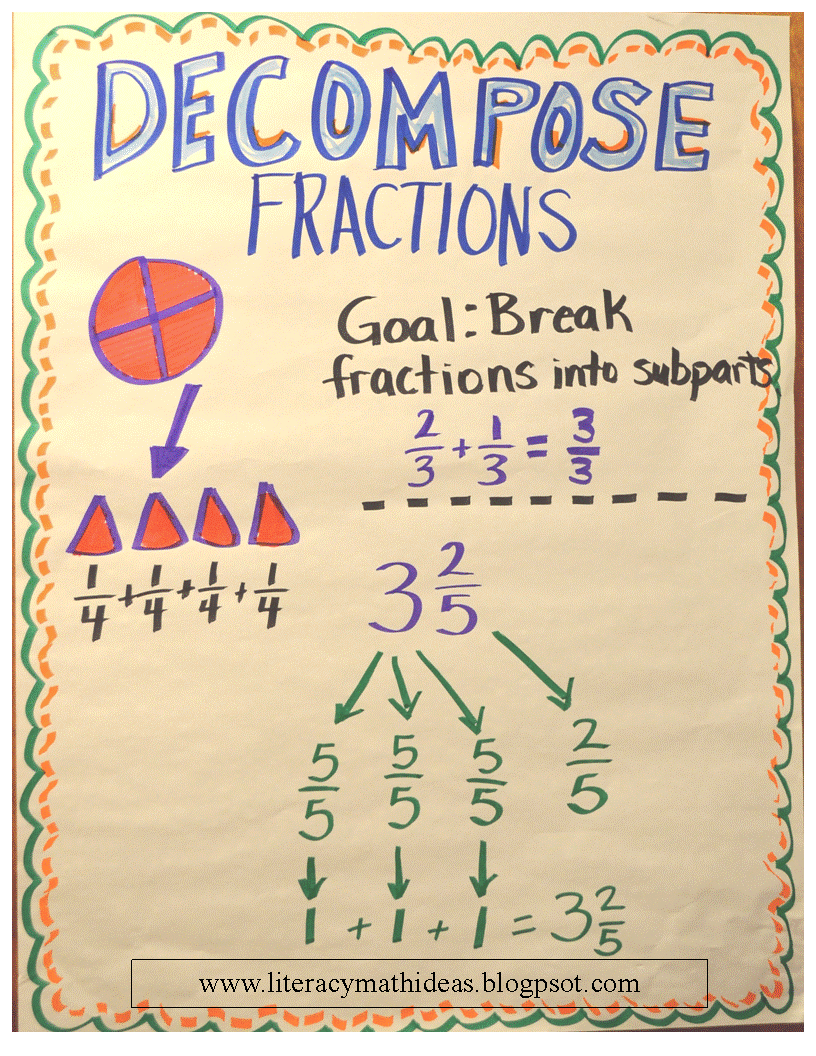
By leaving the task open ended, students reason why there are different possibilities for where the runner’s parents might be during the race. Jan 22, · Decompose fractions as a sum of unit fractions using tape diagrams.
Lesson 4 Concept Development Problem 1: Use tape diagrams to represent the decomposition of 1/3 as the sum of unit fractions. Problem 2: Use tape diagrams to represent the decomposition of 1/5 and 2/5 as the sum of smaller unit fractions.Decomposing a fraction visually (video) | Khan AcademyDecompose a fraction into a sum of fractions using tape diagrams | LearnZillion