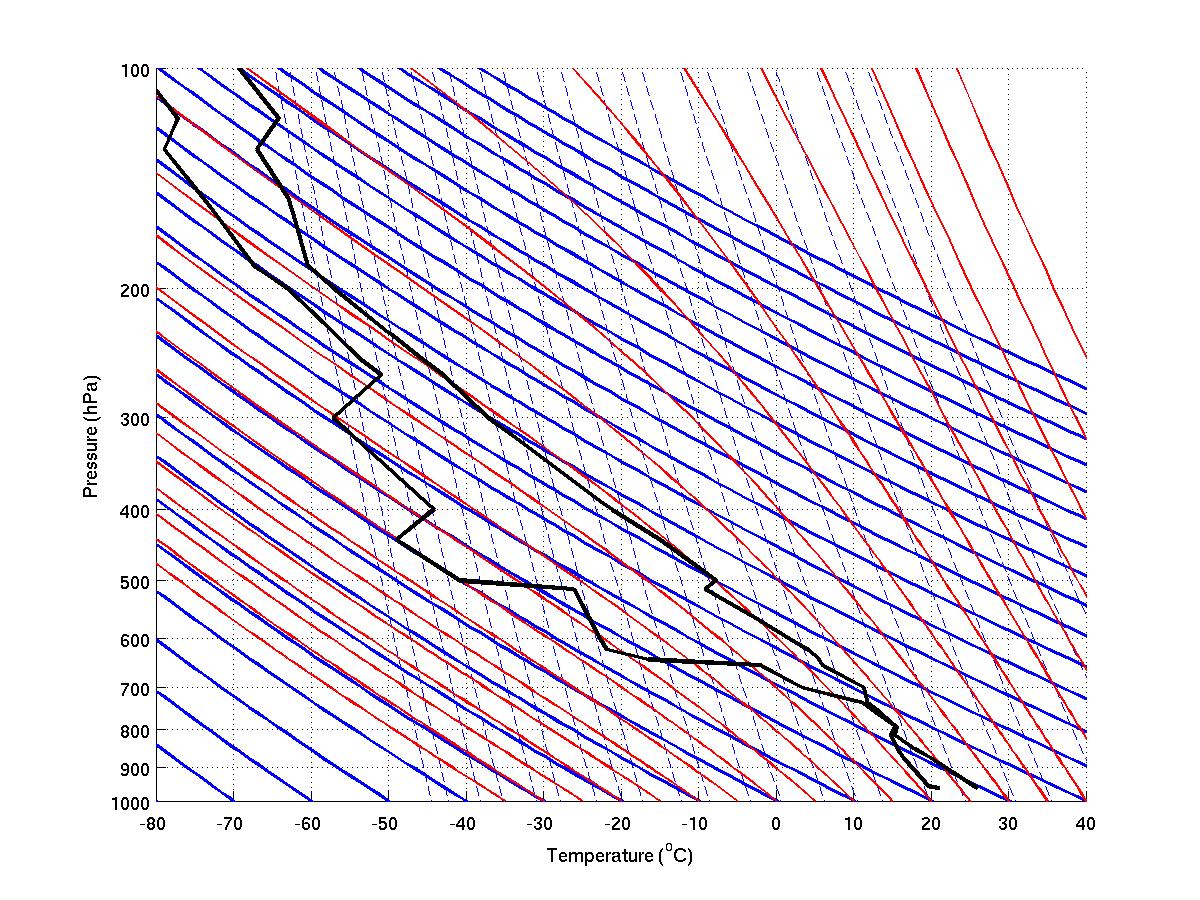

Solid brown lines that run horizontally from left to right and are labeled on the left side of the diagram. Pressure is given in increments of mb and ranges from.
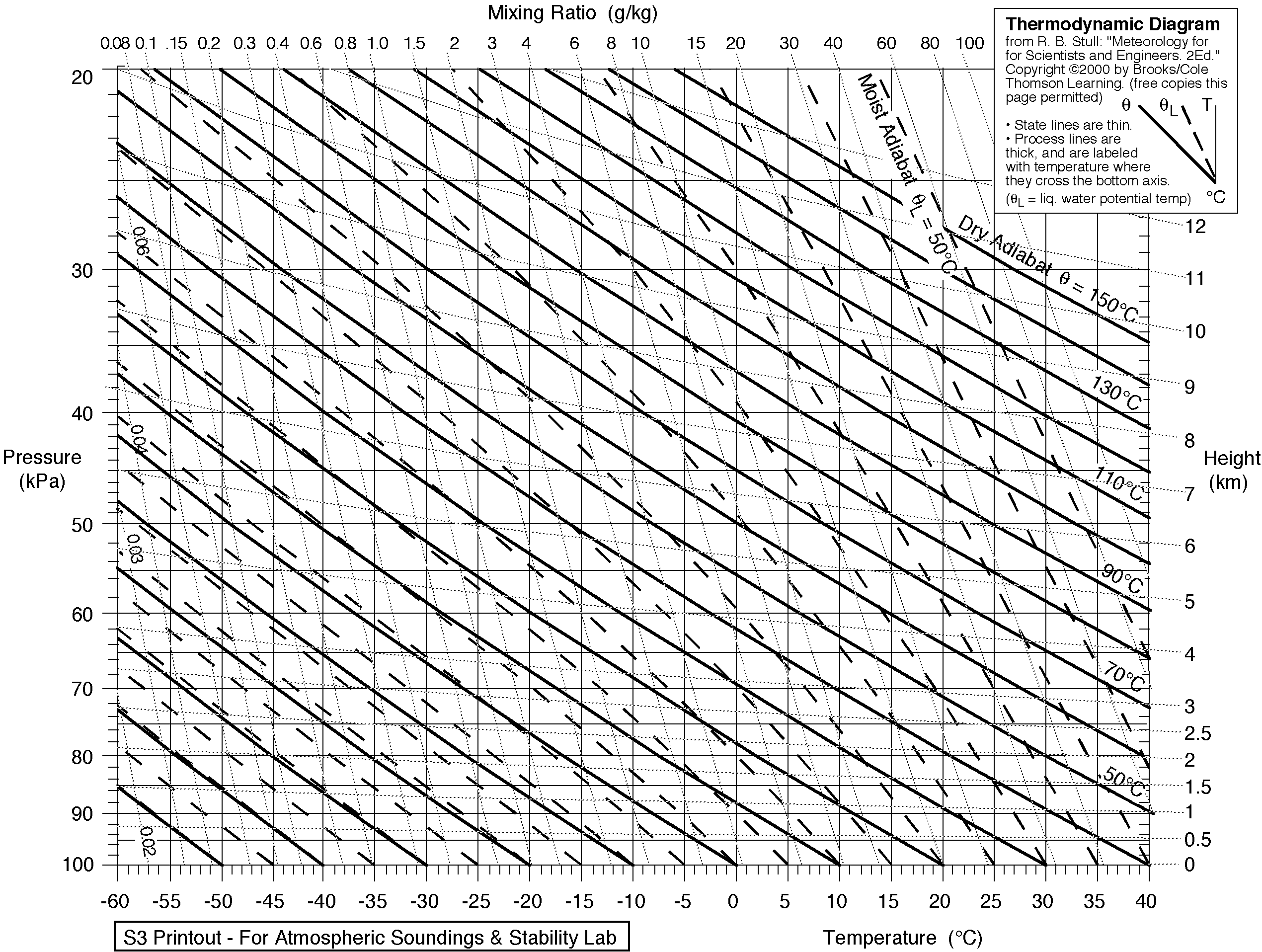
Solid brown lines that run horizontally from left to right and are labeled on the left side of the diagram. Pressure is given in increments of mb and ranges from.
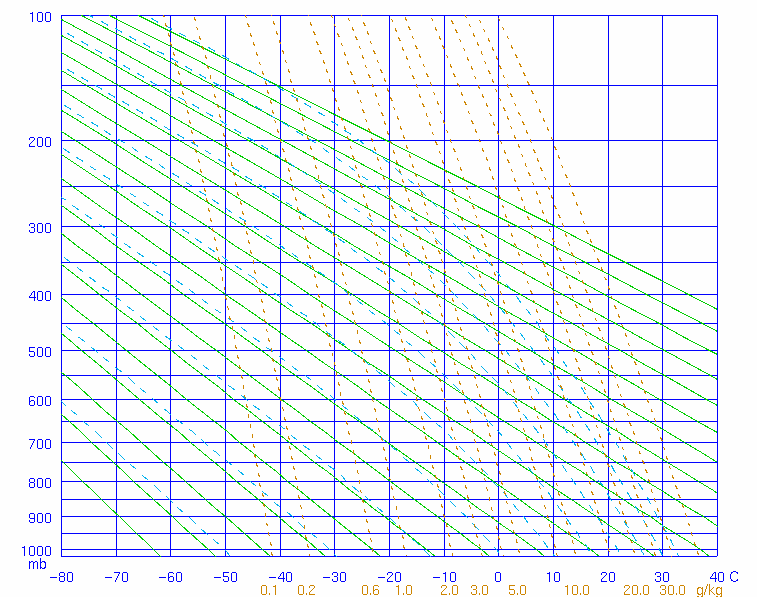
Stuve Diagram. Name: Victor T. Status: student Age: 20s Location: N/A Country: N/A Date: Question: Hi, How do you read a Stuve Diagram?.
Also, the tropopause (the boundary between the troposphere & the stratosphere) is shown to be at about mb. This is the height in the very high levels of the.
Stuve Diagrams are one type of thermodynamic diagram used to then the saturation mixing ratio can be read directly from the chart.For completeness, the dewpoint temperature of the parcel (Td) can be plotted upon the diagram at the same pressure level. 3) Dry adiabats.
The straight, solid, green lines sloping upward to the left on the diagram are called “dry adiabats”. This diagram has a simplicity in that it uses straight lines for the three primary variables: pressure, temperature and potential temperature.
The isotherms are straight and vertical, isobars are straight and horizontal and dry adiabats are also straight and have a 45 degree inclination to the left while moist adiabats are curved. saturated adiabat in the Stuve diagram.
mb layer conditionally unstable (T curve lapse rate lies between the dry adiabatic lapse rate & the saturated adiabatic lapse rate) mb layer absolutely stable (T curve lapse rate. A Stüve diagram with sounding data contains: Temperature sounding data – black jagged line to right.

The temperature scale is given in degrees Celsius along the bottom from C to +40 C. On your Stuve diagram use a colored pen to mark the starting point for the air parcel at a temperature of 22 ° C and a pressure of mb. What is the altitude?

Now mark a point m higher up with a temperature of 10 ° C less.Stüve diagram – WikipediaThermodynamic Diagrams