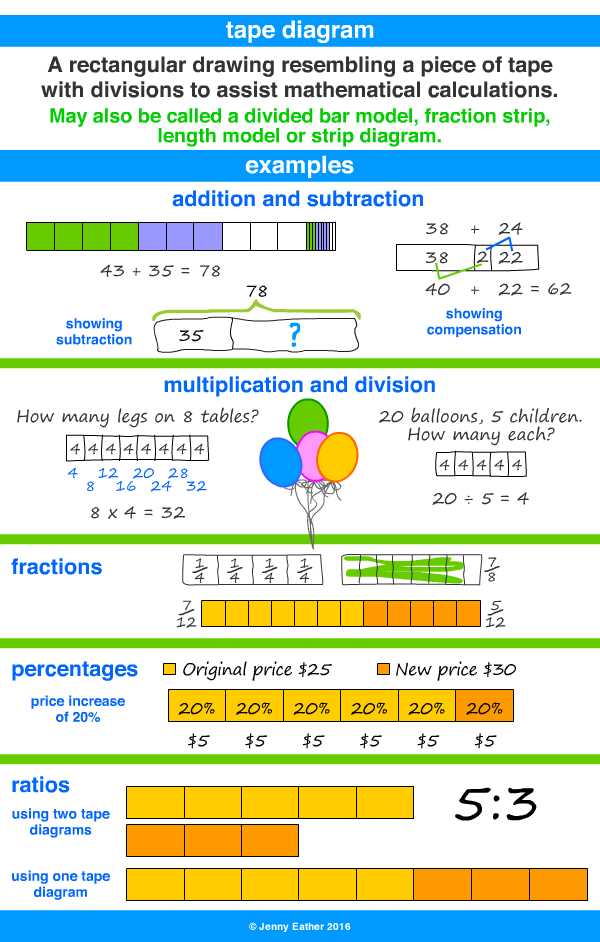
Tape diagram for fractions is a visual representation tool that helps students understand and solve fraction problems. It is also known as a bar model or a strip diagram, and it can be used to illustrate relationships and comparisons between fractions. Using a tape diagram can make abstract concepts more concrete and easier to understand for students of all ages.
A tape diagram consists of a bar or strip that is partitioned into equal parts. Each part represents a specific fraction of the whole bar. The length of each part corresponds to the size or value of the fraction it represents. By looking at the diagram, students can easily compare fractions and determine their relative sizes.
Tape diagrams can be used in a variety of ways to solve fraction problems. For example, students can use a tape diagram to find the sum or difference of two fractions by adding or subtracting the lengths of the corresponding parts. They can also use the diagram to find equivalent fractions by partitioning the bar into different fractions or by multiplying or dividing the lengths of the parts.
Tape Diagram for Fractions
A tape diagram is a visual tool that helps us to solve and understand fractions. It uses a rectangular bar or tape to represent the whole, and it is divided into equal parts, with each part representing a fraction. The tape diagram allows us to see the relationship between the whole and the parts, as well as the relationship between different fractions.
When working with fractions, tape diagrams can be used to illustrate addition, subtraction, multiplication, and division. For example, if we want to add 1/4 and 2/3, we can use a tape diagram to represent both fractions. We divide the tape into 4 equal parts and shade 1 part to represent 1/4, and then we divide it into 3 equal parts and shade 2 parts to represent 2/3. By counting the shaded parts, we can see that the sum is 11/12.
Tape diagrams can also be used to compare fractions. For example, if we want to compare 1/2 and 3/4, we can use a tape diagram to represent both fractions. We divide the tape into 2 equal parts and shade 1 part to represent 1/2, and then we divide it into 4 equal parts and shade 3 parts to represent 3/4. By comparing the shaded parts, we can see that 3/4 is greater than 1/2.
In addition to solving problems, tape diagrams can also help us develop a conceptual understanding of fractions. They allow us to see fractions as parts of a whole and help us visualize and reason about fraction operations. Whether we are adding, subtracting, multiplying, or dividing fractions, a tape diagram can provide a clear and visual representation of the problem, making it easier to solve and understand.
What is a Tape Diagram?
A tape diagram is a visual representation used to solve math problems involving fractions. It is also known as a bar model or a strip diagram. It helps students understand and solve complex fraction problems by breaking them down into simpler parts.
The tape diagram consists of a horizontal or vertical bar that is divided into equal parts. Each part represents a fraction or a specific quantity. The length of the bar can represent the whole or a unit, and the parts of the bar represent the fractions or quantities involved in the problem.
Tape diagrams are particularly helpful when comparing fractions or finding equivalent fractions. They allow students to visualize the relationship between different fractions and make it easier to understand the concepts of multiplication and division with fractions. By using tape diagrams, students can see how fractions are composed and decomposed, which helps them develop a deeper understanding of fraction operations.
Using Tape Diagrams to Solve Fractions Problems

Fractions can sometimes be challenging to understand and solve, especially when working with word problems. However, one helpful tool that can make this process easier is a tape diagram. A tape diagram is a visual representation that allows us to see and solve fractions problems more clearly.
When using a tape diagram for fractions, we start by drawing a long rectangle or “tape” to represent the whole quantity or unit. This tape is then divided into equal parts to represent the fractions involved in the problem. Each part of the tape represents one unit or one whole.
For example, let’s say we have a problem that asks us to find the sum of 1/3 and 1/4. We can draw a tape diagram with three equal parts to represent 1/3 and four equal parts to represent 1/4. By visualizing these fractions on the tape diagram, we can see that 1/3 is smaller than 1/4. To find the sum, we need to find a common denominator and add the parts together.
Using a tape diagram can help us better understand fractions and solve problems more effectively. It allows us to visualize the relationships between different fractions and make connections between the parts and the whole. By breaking down the problem into smaller, more manageable parts, we can work through fractions problems step by step and arrive at the correct solution. So next time you encounter a fractions problem, try using a tape diagram to make the process easier and more intuitive.
Visualizing Fractions with Tape Diagrams

One effective way to understand and work with fractions is to use tape diagrams. Tape diagrams are visual representations that help us to visualize and solve problems involving fractions. They can be used to represent the different parts of a whole, as well as the relationship between the parts and the whole.
Tape diagrams can be especially helpful when comparing fractions or adding and subtracting fractions. For example, if we have a tape diagram that represents a whole pizza, we can divide the diagram into equal parts to represent different fractions of the pizza. Each part of the tape diagram can then be labeled with the corresponding fraction.
For example:
- A tape diagram divided into 8 equal parts can represent the fraction 1/8 of the whole pizza.
- A tape diagram divided into 4 equal parts can represent the fraction 1/4 of the whole pizza.
By using tape diagrams, we can easily compare these fractions and see that 1/4 is larger than 1/8, because the tape diagram representing 1/4 is divided into fewer parts than the tape diagram representing 1/8. This visual representation can help us understand the concept of fractions and make it easier to solve problems involving fractions.
In addition to comparing fractions, tape diagrams can also be used to add and subtract fractions. We can combine tape diagrams representing different fractions to find the sum or difference of the fractions. By visually adding or subtracting the parts of the tape diagram, we can determine the new fraction that represents the result.
Overall, tape diagrams provide a powerful tool for visualizing and solving problems involving fractions. Whether it’s comparing fractions, adding and subtracting fractions, or simply understanding the concept of fractions, tape diagrams can help make the process easier and more intuitive.
Benefits of Using Tape Diagrams for Fractions
When it comes to understanding fractions, tape diagrams can be a valuable tool. These visual representations can help students grasp the concept of fractions and make solving problems involving fractions much easier. Here are some benefits of using tape diagrams for fractions:
1. Visual Representation: Tape diagrams provide a visual representation of fractions, making it easier for students to understand the relationship between the numerator and the denominator. This visual aid can help them visualize the fractions as parts of a whole or as a comparison between two quantities.
2. Problem Solving: Tape diagrams can be particularly helpful when solving fraction-related problems. Students can use the tape diagram to set up the problem and visually identify the information given. This can make problem-solving more systematic and less confusing.
3. Conceptual Understanding: Tape diagrams can enhance students’ conceptual understanding of fractions. By using tape diagrams, students can see how fractions can be represented in different ways, such as as a part of a whole, a part of a set, or a part-to-part comparison. This deepens their understanding of the concept and helps them make connections between different representations of fractions.
4. Flexible Learning: Tape diagrams are a versatile tool that can be used in various ways to teach fractions. They can be used for introducing the concept of fractions, reinforcing understanding, or even as a diagnostic tool to identify areas where students may be struggling. The flexibility of tape diagrams allows teachers to adapt their instruction to meet the needs of their students.
5. Engaging and Interactive: Tape diagrams can make learning fractions more engaging and interactive. Students can actively participate by drawing and labeling the diagram, manipulating the parts, and discussing their findings. This hands-on approach to learning fractions can increase student engagement and improve their retention of the material.
In conclusion, tape diagrams offer several benefits when it comes to teaching and learning fractions. They provide a visual representation, aid in problem-solving, enhance conceptual understanding, offer flexibility in instruction, and promote engagement and interactivity. By incorporating tape diagrams into fraction lessons, educators can help their students develop a solid foundation in this important mathematical concept.
Tips for Using Tape Diagrams Effectively
Tape diagrams are a powerful visual tool that can help students understand and solve mathematical problems involving fractions. To use tape diagrams effectively, it is important to keep in mind a few key tips.
1. Start with a clear problem statement:
Before creating a tape diagram, make sure you clearly understand the problem. Identify the key information and what the problem is asking you to find. This will help you determine what elements to include in your diagram.
2. Use labels effectively:
Labels are important in tape diagrams to represent different parts of a whole. Clearly label the different sections or parts of the diagram to avoid confusion. For example, if the problem involves dividing a rectangle into equal parts, label each section with the fraction it represents.
3. Maintain consistency:
When using tape diagrams, it is important to maintain consistency in terms of the scale and proportions. Use the same size and shape of boxes or rectangles to represent equal parts. This will help students make accurate comparisons and calculations.
4. Encourage students to think multiplicative:
One of the advantages of tape diagrams is that they can help students think multiplicative rather than just additive. Encourage students to see the relationship between the lengths or areas of different parts in terms of multiplication. This can deepen their understanding of fractions.
5. Practice, practice, practice:
Like any mathematical tool, tape diagrams require practice. Encourage students to regularly use tape diagrams to solve fraction problems. The more they practice, the more comfortable and proficient they will become in using this visual approach.
By following these tips, students can effectively use tape diagrams to solve fraction problems and gain a stronger understanding of mathematical concepts.
Examples of Solving Fractions Problems with Tape Diagrams
Tape diagrams are a helpful visual tool for solving fraction problems. They allow us to represent fractions using segments of a tape, making it easier to understand and solve problems involving fractions.
Here are some examples of how tape diagrams can be used to solve fraction problems:
- Example 1: Sarah has a ribbon that is 3/8 of a yard long. She wants to cut it into equal pieces for a craft project. How long should each piece be?
- Example 2: Tom has 3/4 of a pizza left. He wants to share it equally with his 4 friends. How much pizza should each person get?
To solve this problem, we can use a tape diagram. We draw a tape and divide it into 8 equal segments to represent the whole ribbon. Then, we shade in 3 segments to represent the length of the ribbon that Sarah has.

From the diagram, we can see that each segment represents 1/8 of a yard. Since Sarah has 3 segments shaded, the length of each piece should be 3/8 of a yard.
Again, we can use a tape diagram to solve this problem. We draw a tape and divide it into 4 equal segments to represent the number of friends. Then, we shade in 3 segments to represent the amount of pizza that Tom has.

From the diagram, we can see that each segment represents 1/4 of a pizza. Since Tom has 3 segments shaded, each person should get 3/4 divided by 4, which is 3/16 of a pizza.
These examples demonstrate how tape diagrams can help us visualize and solve fraction problems. By breaking down the problem into visual segments, we can better understand the concept of fractions and find the solution more easily.
Tape diagrams are a valuable tool for students learning fractions, as they provide a visual representation that aids in problem-solving and comprehension. They can be used to solve various types of fraction problems, including addition, subtraction, multiplication, and division.
Next time you encounter a fraction problem, try using a tape diagram to simplify the problem and find the solution!