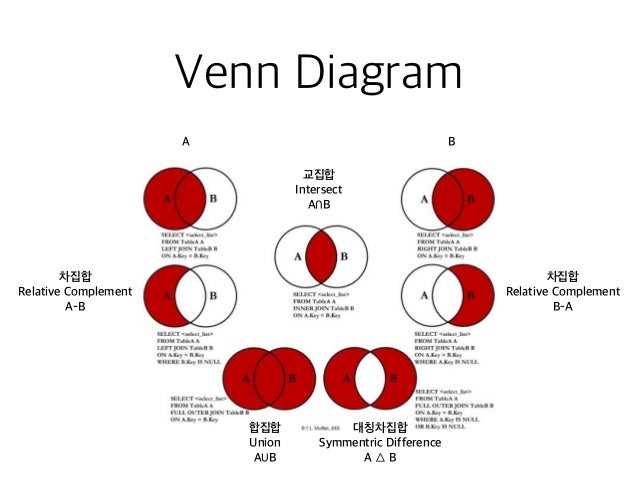
The Venn diagram is a powerful tool used in mathematics and logic to visualize the relationships between sets. It consists of overlapping circles that represent different sets, and the areas where the circles overlap show the intersection of those sets. One common type of Venn diagram is the A intersect B complement diagram, which illustrates the elements that are in set A, but not in set B.
In this type of Venn diagram, set A is represented by one circle and set B by another circle that overlaps with A. The area outside both circles represents the complement of A intersect B, meaning the elements that are in A but not in B.
To create an A intersect B complement Venn diagram, start by drawing two circles that overlap partially. Label one circle as set A and the other as set B. Then, shade the area outside both circles to represent the complement of A intersect B. This shaded area shows the elements that are only in set A and not in set B.
What is a Venn diagram?
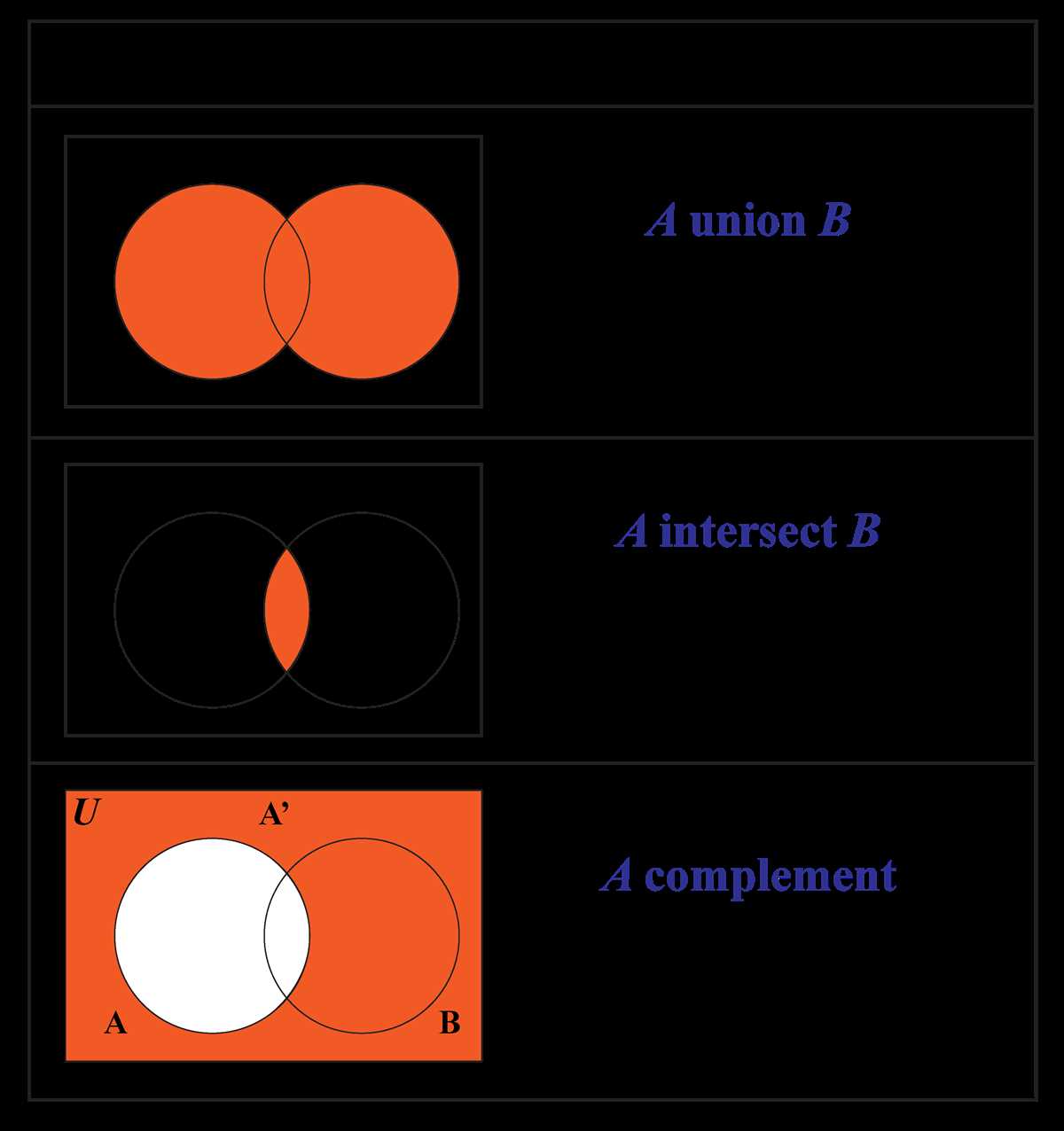
A Venn diagram is a graphical representation of the relationships between different sets of data. It was introduced by the mathematician John Venn in the late 19th century as a way to depict logical relationships and set theory.
The diagram consists of overlapping circles or ellipses, each representing a set or a category. The areas of overlap between the circles show the elements that belong to multiple sets. The non-overlapping areas represent the elements that belong to only one set.
A Venn diagram can be used to compare and contrast different sets, identify the common elements, and illustrate the relationships between them. It is commonly used in mathematics, logic, statistics, and various other fields to visually organize and analyze data.
One popular use of a Venn diagram is to represent the intersection and complement of two sets. The intersection refers to the elements that are common to both sets, while the complement refers to the elements that belong to one set but not the other.
Overall, a Venn diagram provides a clear and concise way to visualize the relationships between sets and analyze data, making it a valuable tool in various fields of study and research.
How to draw a Venn diagram?
Venn diagrams are a useful tool for visualizing relationships between sets. They are commonly used in mathematics, logic, and statistics. Drawing a Venn diagram can be done by following a few simple steps:
Step 1: Start by drawing a rectangle or a circle to represent the universal set, which is the set that contains all the objects or elements under consideration.
Step 2: Identify the sets you want to analyze and draw circles or ovals to represent them within the universal set. Each circle or oval should be labeled with the name or symbol of the set it represents.
Step 3: Determine the overlapping regions if there are any. These regions represent elements that belong to both sets. Draw these overlapping regions as overlapping sections of the circles or ovals.
Step 4: If you want to represent the complement of a set (the elements that do not belong to that set), draw a separate region outside of the circles or ovals to represent the complement. Label this region accordingly.
Step 5: Finally, label the various regions of the Venn diagram to indicate what they represent. This will help clarify the relationships between the sets and their elements.
Venn diagrams are a versatile tool that can be used to analyze and compare sets of any size or complexity. They can be drawn by hand or using software programs, and can be customized to suit specific needs. By following these steps, you can create clear and informative Venn diagrams to help visualize relationships between sets.
Understanding Set Operations
In the study of sets, there are several operations that allow us to combine, compare, and analyze sets. These set operations include intersection, union, complement, and difference. Each operation provides a unique way of manipulating sets and understanding the relationships between them.
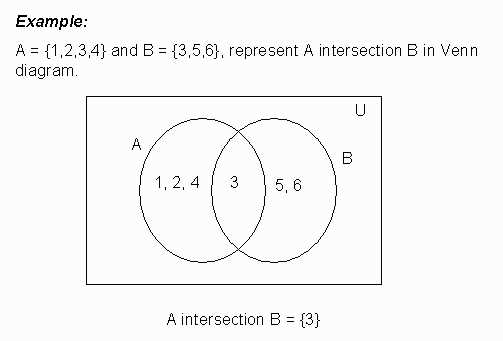
Intersection: The intersection of two sets, A and B, is the set of elements that are common to both sets. In a Venn diagram, the intersection is represented by the overlapping region between the two circles representing the sets. The intersection operation is denoted by the symbol ∩. For example, if A = {1, 2, 3} and B = {2, 3, 4}, then A ∩ B = {2, 3}, as these are the elements that appear in both sets.
Complement: The complement of a set, A, with respect to a universal set, U, is the set of elements that belong to U but not to A. In other words, it is the set of elements that are not in A. The complement operation is denoted by the symbol A’. For example, if U is the set of all whole numbers, and A = {1, 2, 3}, then A’ = {4, 5, 6, …}, as these are the numbers that are not in A.
These set operations, along with union and difference, provide a powerful toolkit for analyzing and manipulating sets. By understanding how these operations work, we can gain insights into the relationships between sets and solve various mathematical problems.
What is A intersect B complement?
The intersection of two sets A and B, denoted as A ∩ B, represents the elements that are common to both sets. In other words, it is the set of elements that belong to both sets A and B at the same time. On the other hand, the complement of a set A, denoted as A’, represents all the elements that do not belong to set A.
When we talk about A intersect B complement, we are referring to the set of elements that belong to both sets A and B but do not belong to set B. In other words, it is the set of elements that are common to both sets A and B, but exclusive to set A.
This concept is often represented in a Venn diagram, which is a graphical illustration that uses circles to represent sets. In the Venn diagram for A intersect B complement, the circles A and B would overlap, representing the intersection A ∩ B. However, the portion of A that is outside of B would be shaded or marked differently to indicate that it represents the complement of B.
Understanding the concept of A intersect B complement is useful in various mathematical and logical applications. It allows us to analyze and compare sets, identify shared elements, and differentiate them from the elements that are exclusive to each set.
Applying A intersect b complement to a Venn diagram
In the context of set theory, the concept of A intersect b complement can be visually represented using a Venn diagram. A Venn diagram is a graphical representation of sets, where each set is represented by a circle and the overlapping regions represent the intersection of sets.
To apply A intersect b complement to a Venn diagram, we first identify the sets A and B, and then draw two circles to represent these sets. The overlapping region between the two circles represents the intersection of A and B, which is denoted as A intersect B.
To represent the complement of A intersect B, we need to shade the region outside the intersection. This region consists of all the elements that do not belong to both sets A and B. By shading this region, we visually indicate the complement of A intersect B.
By using A intersect b complement in a Venn diagram, we can gain a better understanding of the relationship between the sets A and B. It allows us to visualize the elements that are not part of the intersection and helps in analyzing the differences and similarities between the two sets.
In conclusion, applying A intersect b complement to a Venn diagram provides a visual representation of the complement of the intersection between sets A and B. By shading the region outside the intersection, we can better understand the relationship between the two sets and identify the elements that do not belong to both sets.
Interpreting the results of A intersect b complement
After analyzing the Venn diagram representing the intersection of sets A and B complement, it is important to interpret the results to gain a better understanding of the relationship between the two sets. The A intersect B complement represents the elements that are in set A but not in set B.
Interpretation:
- If an element is in set A intersect B complement, it means that the element is part of set A, but not part of set B.
- The intersection of sets A and B complement can be seen as the set of elements that are exclusive to set A.
- Elements in set A intersect B complement do not overlap with set B.
It is important to note that the interpretation of the results will depend on the context and the specific sets A and B being analyzed. The results can provide valuable insights into the differences and distinctions between the two sets, helping to identify unique elements in set A.
Q&A:
What is A intersect B complement?
A intersect B complement refers to the set of elements that are in set A but not in set B.
How do you interpret the results of A intersect B complement?
The results of A intersect B complement show the elements that are present in set A but not in set B.
What is the relationship between A intersect B complement and set difference?
A intersect B complement is equivalent to set difference of set A and set B.
What does it mean if A intersect B complement is an empty set?
If A intersect B complement is an empty set, it means that all elements of set A are also present in set B.
Can A intersect B complement be an infinite set?
Yes, A intersect B complement can be an infinite set if both set A and set B are infinite sets.
What does “A intersect B complement” mean?
“A intersect B complement” refers to the set of elements that are in set A but not in set B.