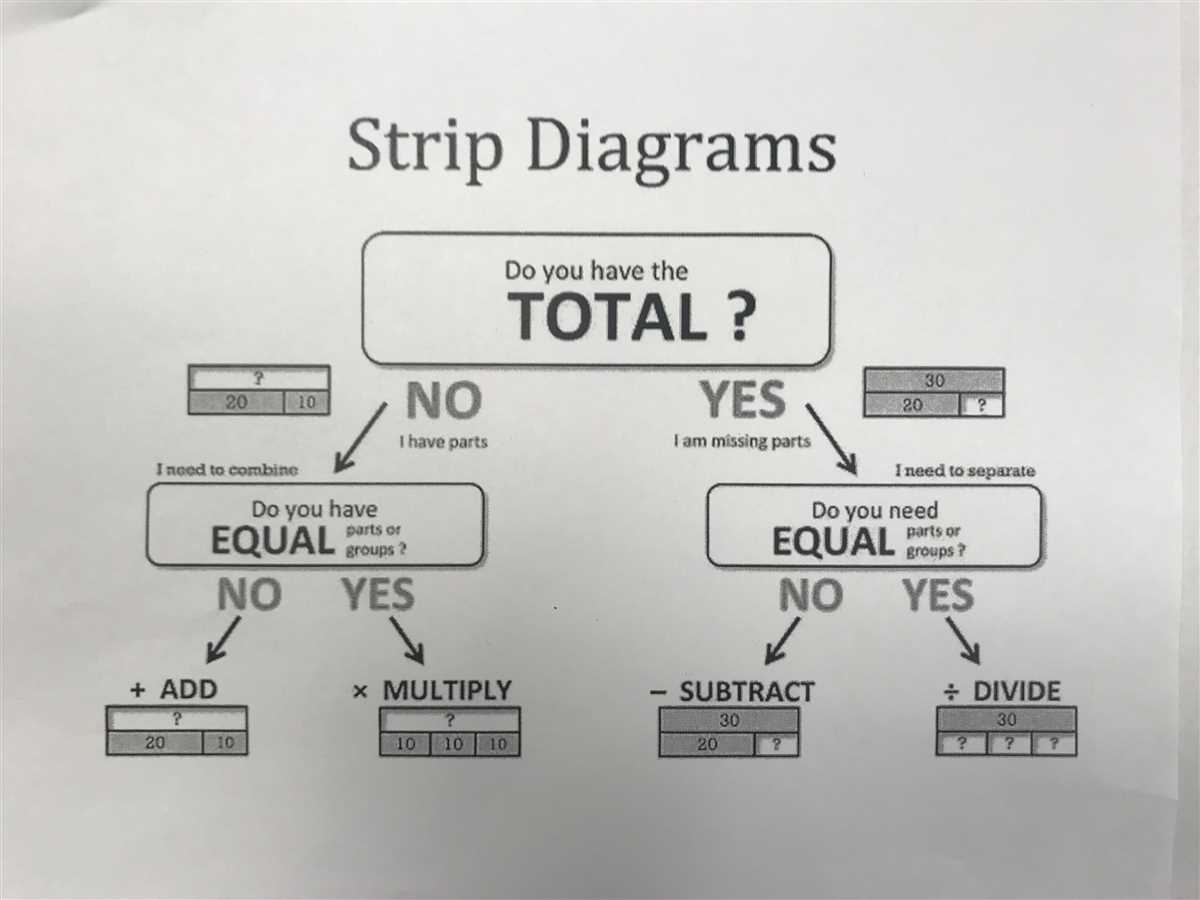
A multiplication tape diagram, also known as a strip diagram, is a visual representation used to solve multiplication problems. It is commonly used in elementary math classrooms to help students understand and solve multiplication equations. The diagram consists of a strip or tape divided into equal parts, with each part representing a specific quantity or number. By using the tape diagram, students can visualize the relationship between the numbers being multiplied and determine the product.
The multiplication tape diagram is a powerful tool in teaching multiplication because it helps students understand the concept of multiplication as repeated addition. By breaking down the multiplication equation into equal parts, students can see how the numbers are related and how they come together to form the product. This visual representation also allows students to easily manipulate the numbers and see the effects of multiplying different quantities.
In addition to helping students understand the concept of multiplication, the tape diagram can also be used to solve more complex multiplication problems. By breaking down the problem into smaller parts and using the diagram to visualize the relationship between the numbers, students can easily solve multi-digit multiplication problems. This method not only helps students see the steps involved in solving the problem but also reinforces their understanding of place value and the properties of multiplication.
In conclusion, the multiplication tape diagram is a valuable tool in teaching multiplication. By providing a visual representation of the relationship between the numbers being multiplied, it helps students understand and solve multiplication equations. Whether used to introduce multiplication to young learners or to solve complex problems, the tape diagram is an effective way to support students’ understanding of multiplication.
Multiplication Tape Diagram
A multiplication tape diagram is a visual representation that helps students understand the concept of multiplication. It consists of a number line or a rectangular strip divided into equal parts, with each part representing a specific quantity. The tape diagram is typically used to solve word problems involving multiplication, as it provides a visual representation of the problem and helps students make sense of the problem-solving process.
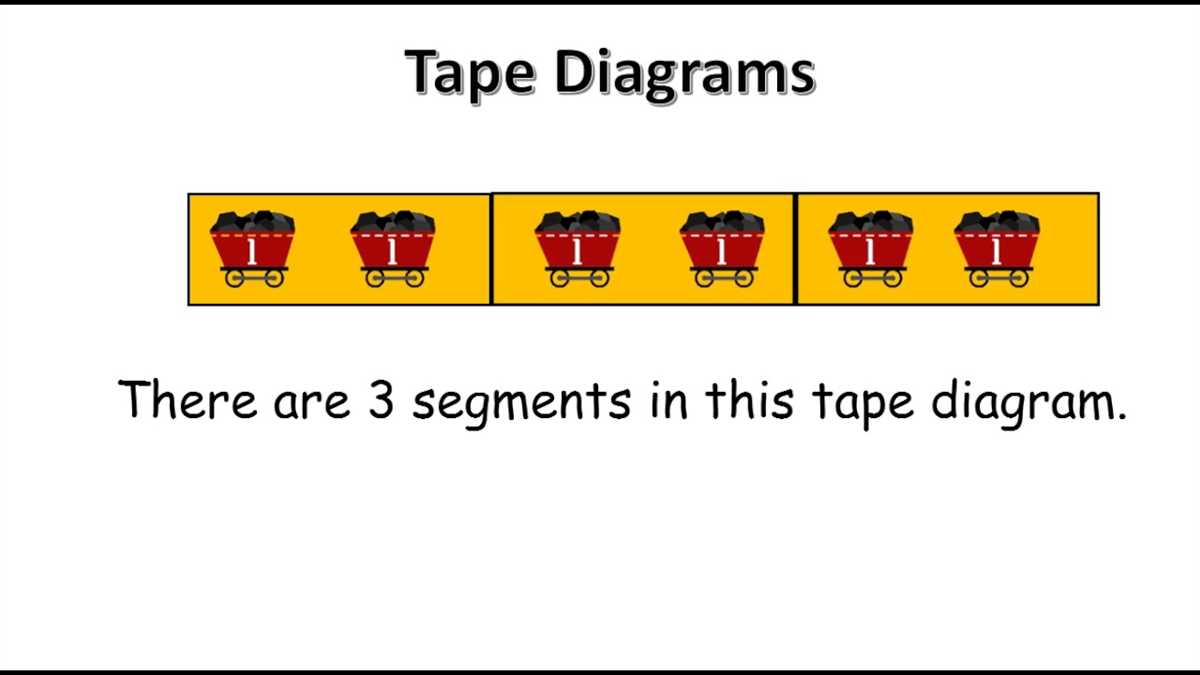
In a multiplication tape diagram, the total number being multiplied is represented by the length of the tape or the number line. For example, if the problem states “Three bags of marbles are being multiplied by four marbles in each bag,” the tape diagram would show three equal sections to represent the bags, with each section divided into four smaller parts to represent the marbles in each bag. The diagram visually represents the multiplication process: 3 bags × 4 marbles = 12 marbles in total.
Tape diagrams can also be used to solve more complex multiplication problems. For example, if the problem states “Five students each brought six pencils for a total of pencils,” the tape diagram would show five equal sections to represent the students, with each section divided into six smaller parts to represent the pencils. The diagram visually represents the multiplication process: 5 students × 6 pencils = 30 pencils in total.
Using a multiplication tape diagram helps students develop a conceptual understanding of multiplication by providing a concrete representation of the problem. It allows students to see the relationship between the numbers being multiplied and the total product, making it easier for them to solve word problems and grasp the underlying mathematical concepts.
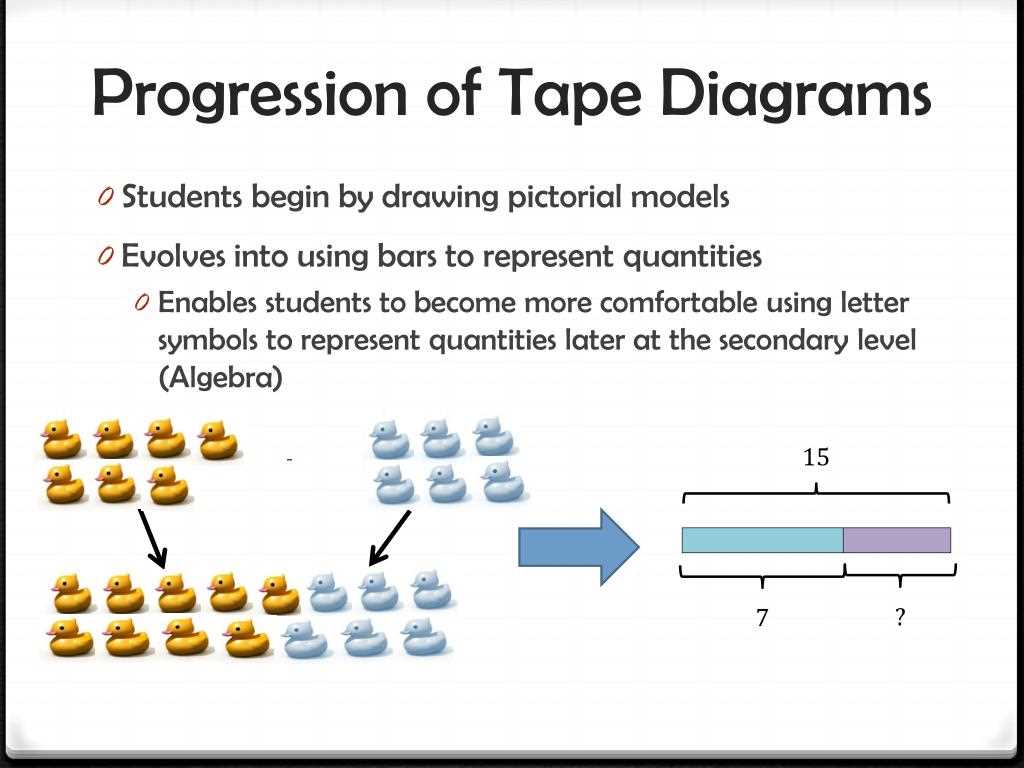
What is a Tape Diagram?
In mathematics, a tape diagram is a visual representation used to solve word problems. It is a way to organize and illustrate information in order to better understand the problem and find a solution. Tape diagrams are particularly useful for understanding relationships between quantities and solving problems involving multiplication.
A tape diagram consists of a line or rectangle that is divided into equal segments, with each segment representing a specific quantity or value. The segments are labeled with numbers or symbols to indicate the quantities involved in the problem. The diagram can also include additional information such as labels, arrows, and written explanations to provide further clarity.
Tape diagrams can be used for a variety of mathematical operations, but they are especially helpful for multiplication problems. By representing the quantities involved in a multiplication problem on a tape diagram, students can easily visualize and compare the different quantities. This visual representation can help students make sense of the problem, identify patterns, and determine the correct solution.
For example, consider the problem: “Maria has 4 bags of apples, with 6 apples in each bag. How many apples does she have in total?” This problem can be represented using a tape diagram with four segments representing the four bags of apples, and each segment divided into six smaller segments representing the six apples in each bag. By counting the total number of smaller segments, the solution to the problem can be determined.
Understanding Multiplication using Tape Diagrams
Multiplication is a mathematical operation that involves combining two or more numbers to find their total value. It is often represented using symbols such as the ‘x’ or ‘*’, and it is an essential skill in various areas of mathematics, including arithmetic, algebra, and geometry. One effective visual tool for understanding multiplication is a tape diagram.
A tape diagram, also known as a bar model or strip diagram, is a visual representation that uses rectangular bars to show the relationship between different quantities. In the context of multiplication, tape diagrams help students to visualize the process of combining equal groups or sets. The length or area of each bar represents the size or quantity of the group, and the total length or area of the bars represents the product of the multiplication.
For example, consider the multiplication problem: “There are 5 bags, and each bag has 6 marbles. How many marbles are there in total?” To solve this problem using a tape diagram, a student would draw five bars of equal length to represent the five bags. Then, within each bar, they would divide it into six equal segments to represent the six marbles in each bag. The total length of all the bars combined would give them the total number of marbles, which in this case would be 30.
Tape diagrams are particularly helpful for students who are visual learners or struggle with abstract concepts. They provide a concrete and visual representation of the multiplication process, allowing students to better understand and solve multiplication problems. By using tape diagrams, students can develop a deeper conceptual understanding of multiplication and build a solid foundation for further mathematical learning.
Steps to Solve Multiplication Problems with Tape Diagrams

When solving multiplication problems using tape diagrams, it is important to follow a few key steps. These steps will help ensure that you accurately represent the problem and find the correct solution. Here is a breakdown of the process:
Step 1: Understand the Problem
The first step in solving multiplication problems with tape diagrams is to carefully read and understand the problem. Identify the key information such as the numbers involved, the quantities being multiplied, and any additional context provided. This will give you a clear understanding of what you need to solve for.
Step 2: Represent the Problem with a Tape Diagram
After understanding the problem, create a tape diagram to visually represent the quantities involved. A tape diagram is a way to illustrate the relationship between different quantities using rectangular bars. Label the known quantities and any unknowns using appropriate numbers or variables. This diagram will serve as a visual guide throughout the problem-solving process.
Step 3: Partition and Distribute the Quantities
Next, divide the known quantities into smaller equal parts based on the multiplication factor. Use the tape diagram to help partition the bars or sections accordingly. Distribute the smaller parts equally among the different sections to represent the multiplication process. This step helps to visualize how the quantities are being multiplied together.
Step 4: Determine the Unknown Quantity

Using the tape diagram, identify the section or sections that represent the unknown quantity. Count the number of smaller parts in that section to determine the total value of the unknown. This step helps to solve for the missing information and find the answer to the multiplication problem.
Step 5: Check and Interpret the Solution

Finally, check your solution by verifying that the tape diagram accurately represents the original problem and that the unknown quantity has been correctly determined. Interpret the solution in the context of the problem to ensure that it makes sense. Double-check your calculations if necessary. This step helps to ensure that your answer is correct and meaningful.
By following these steps, you can confidently solve multiplication problems using tape diagrams. The visual representation provided by the tape diagram helps to understand and manipulate quantities, making the multiplication process more accessible and intuitive.
Benefits of Using Tape Diagrams for Multiplication
Tape diagrams are a visual tool that can greatly enhance students’ understanding and mastery of multiplication. These diagrams, also known as bar models, provide a concrete representation of the mathematical concept being taught, making it easier for students to grasp and apply multiplication principles.
One of the main benefits of using tape diagrams for multiplication is that they help students make sense of the problem by breaking it down into smaller parts. By representing the quantities and relationships between them using bars or boxes, students can better understand how multiplication functions and how different factors contribute to the final product.
- Tape diagrams also promote problem-solving skills, as students can use them to analyze and strategize the most efficient way to solve a multiplication problem. They can visually see the numbers they need to work with and the operations they need to perform.
- Additionally, tape diagrams can be used to model and explain various multiplication strategies, such as the distributive property or the use of arrays. Students can see how these strategies can be applied to different problems, helping them develop a deeper conceptual understanding of multiplication.
- Furthermore, tape diagrams provide a visual representation of the multiplication process, allowing students to track their progress and identify any errors or misconceptions they may have. This feedback loop helps students self-correct and learn from their mistakes.
In conclusion, tape diagrams are a valuable tool for teaching and learning multiplication. They provide a visual and concrete representation of multiplication problems, helping students understand the underlying concepts and develop effective problem-solving skills. Incorporating tape diagrams into multiplication instruction can lead to improved comprehension, retention, and mastery of multiplication concepts.
Example Problems

In order to understand the concept of multiplication tape diagrams, let’s look at some example problems.
Example 1: Finding the total number of fruits
Suppose you have 5 baskets, and each basket contains 10 apples. How many apples do you have in total? To solve this problem using a tape diagram, you can draw 5 boxes to represent the baskets. Then, within each box, draw 10 small squares to represent the apples. The boxes indicate the number of baskets, and the squares represent the number of apples in each basket. Counting all the squares, we can see that there are a total of 50 apples.
Example 2: Multiplying fractions
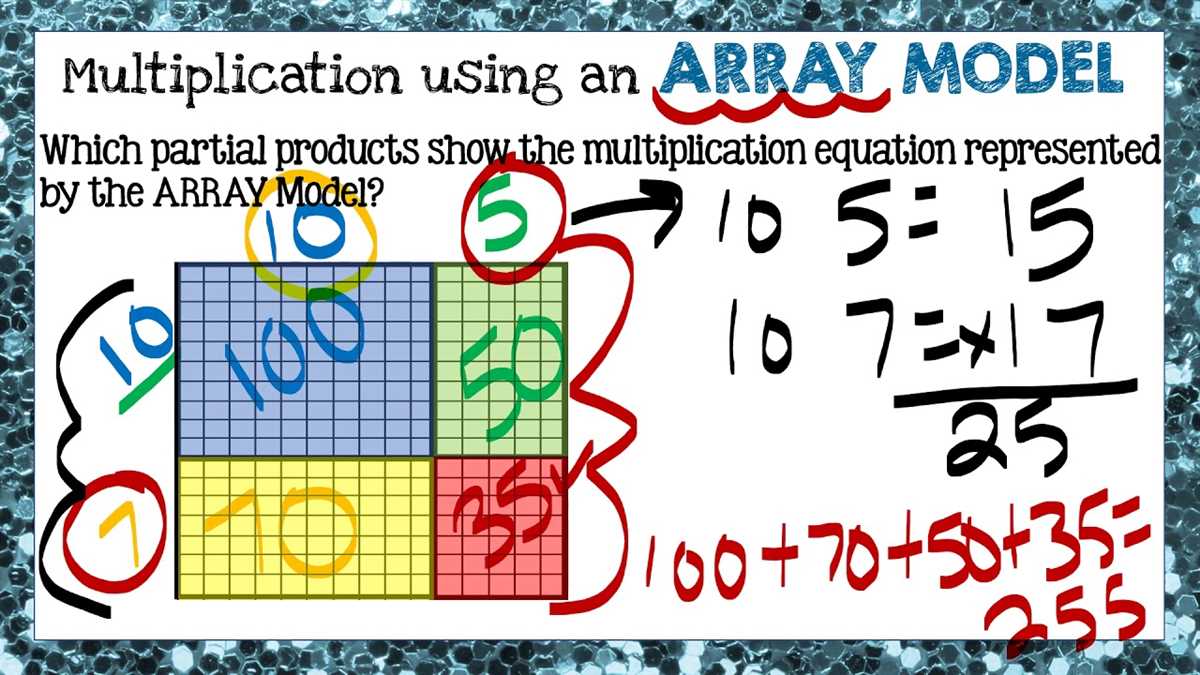
Let’s say you have 3 cakes. Each cake is cut into 4 equal pieces. How many pieces of cake do you have in total? To solve this problem using a tape diagram, you can draw 3 boxes to represent the cakes. Then, within each box, divide it into 4 equal sections to represent the pieces. The number of boxes indicates the number of cakes, and the number of sections represents the number of pieces in each cake. Counting all the sections, we can see that there are a total of 12 pieces of cake.
These example problems demonstrate how tape diagrams can be used to visually represent multiplication situations. By using tape diagrams, students can develop a better understanding of multiplication and solve problems more effectively.
Multiplication Tape Diagram: Practice Exercises
Now that you understand how to use a multiplication tape diagram, it’s time to practice your skills! Below are some exercises that will help you cement your understanding of this visual representation of multiplication.
Exercise 1:

Use a tape diagram to solve the following multiplication problem:
Problem: Jane has 4 equal bags of apples, with 6 apples in each bag. How many apples does she have in total?
| Apples per Bag | Total Bags | Total Apples |
|---|---|---|
| 6 | 4 | ? |
Draw a tape diagram to represent the problem, and then use it to find the total number of apples.
Exercise 2:
Use a tape diagram to solve the following multiplication problem:
Problem: A bakery sells 5 boxes of cookies, with 8 cookies in each box. How many cookies does the bakery sell in total?
| Cookies per Box | Total Boxes | Total Cookies |
|---|---|---|
| 8 | 5 | ? |
Draw a tape diagram to represent the problem, and then use it to find the total number of cookies.
Exercise 3:
Use a tape diagram to solve the following multiplication problem:
Problem: A toy store has 3 shelves, with 10 toys on each shelf. How many toys are there in total?
| Toys per Shelf | Total Shelves | Total Toys |
|---|---|---|
| 10 | 3 | ? |
Draw a tape diagram to represent the problem, and then use it to find the total number of toys.
By practicing these exercises, you will become more comfortable with using tape diagrams to solve multiplication problems. Remember to break down the problem into equal parts and visually represent them in the tape diagram. This will help you understand the concept of multiplication better and improve your problem-solving skills!