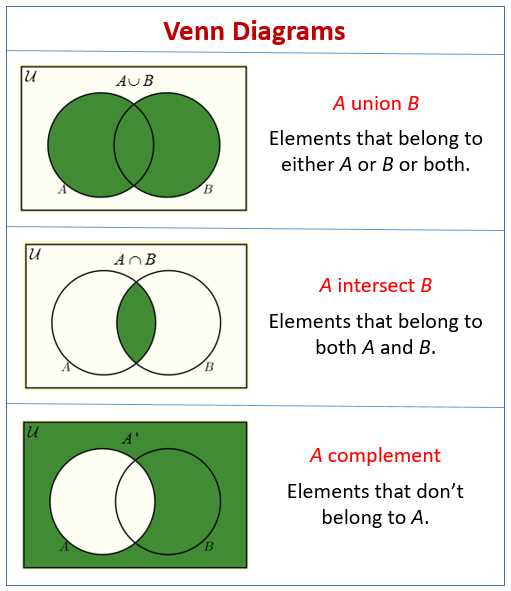
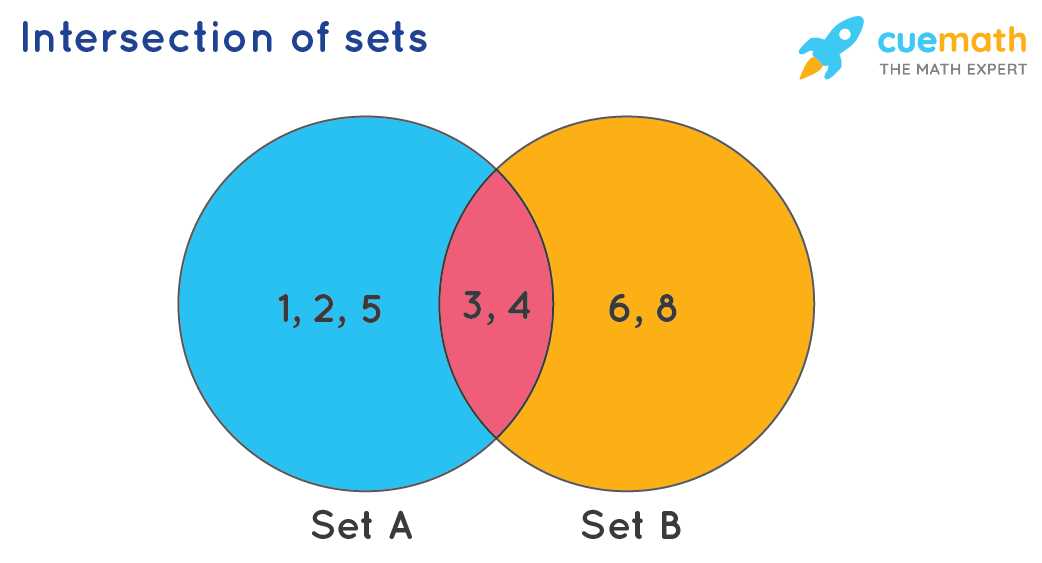
The concept of set theory is widely used in mathematics, applied sciences, and computer science. One of the most basic elements in set theory is the “intersection” of two sets. When we intersect two sets, we are looking for the elements that are common to both sets.
In set theory, the term “complement” refers to the elements that are not in a particular set. In other words, the complement of a set A contains all the elements that are not in set A.
A Venn diagram is a graphical representation of sets using circles or other shapes. In a Venn diagram, the intersection of two sets is represented by the overlapping area of the circles. The complement of a set can be represented by the area outside the circle that represents the set.
The intersection of set A and the complement of set B can be represented in a Venn diagram by shading the overlapping area of the circle representing set A and the area outside the circle that represents set B. This shaded area represents the elements that are in set A but not in set B.
Overview of the A intersection B complement Venn diagram
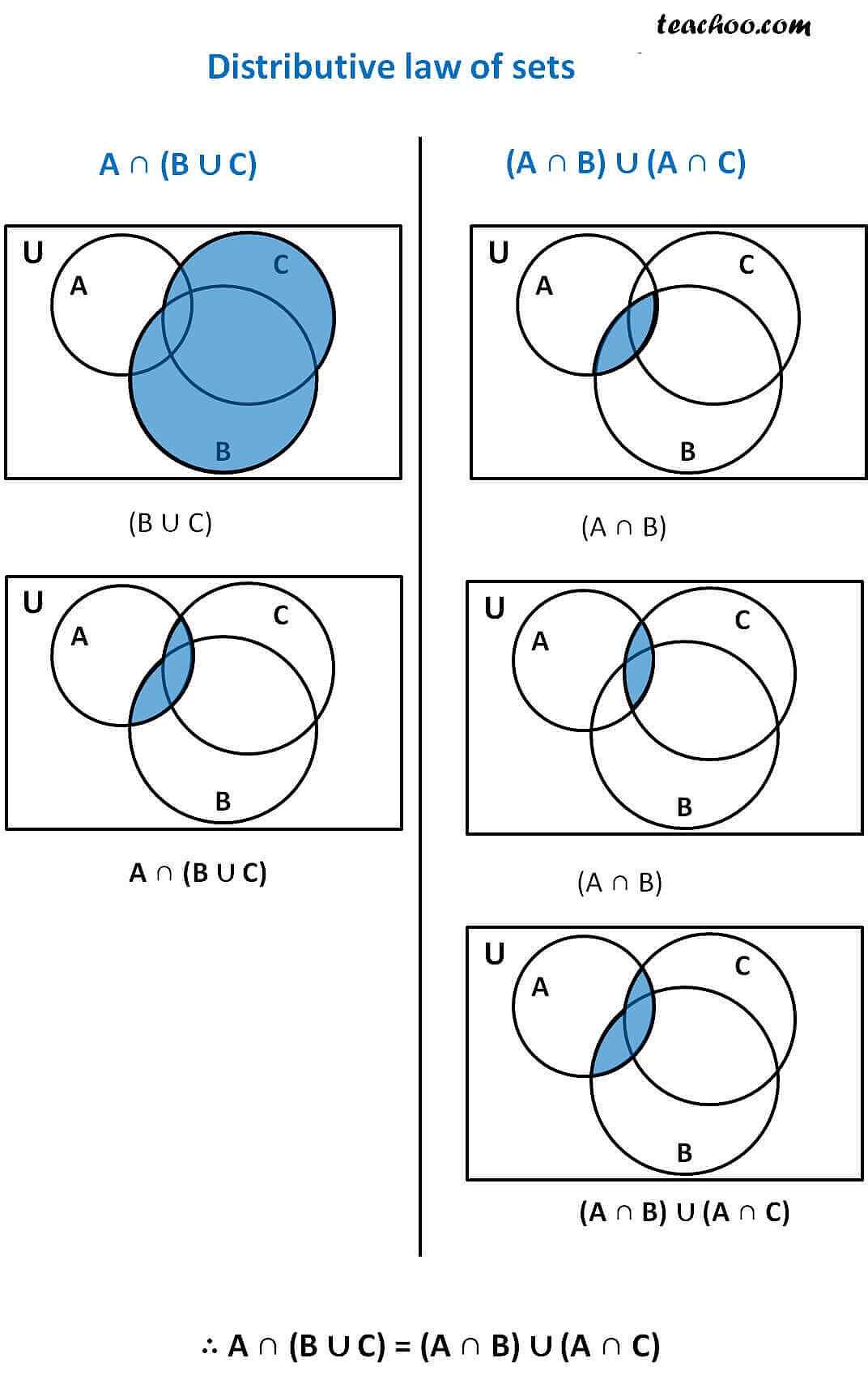
The A intersection B complement Venn diagram is a graphical representation that helps visualize the relationship between two sets, A and B, and their complements. It is a useful tool in set theory and can provide valuable insights into set operations and logic.
The diagram consists of two overlapping circles, one representing set A and the other representing set B. The area where the circles overlap represents the intersection of A and B, while the portions outside the circles represent the complements of A and B.
Key features:
- The intersection of A and B represents the elements that are common to both sets.
- The complement of A (A’) represents the elements that are in the universal set but not in A.
- The complement of B (B’) represents the elements that are in the universal set but not in B.
- The area outside both circles represents the elements that are not in either set A or set B.
The A intersection B complement Venn diagram is particularly helpful when analyzing set operations, such as unions, intersections, and complements. It allows us to visually see the relationships between sets and better understand the outcomes of different operations.
By using the A intersection B complement Venn diagram, we can easily identify elements that belong to certain sets, as well as determine the relationships between sets and their complements. This diagram aids in the logical analysis of set theory and assists in solving problems related to set operations and logic.
Understanding the A intersection B complement Venn diagram
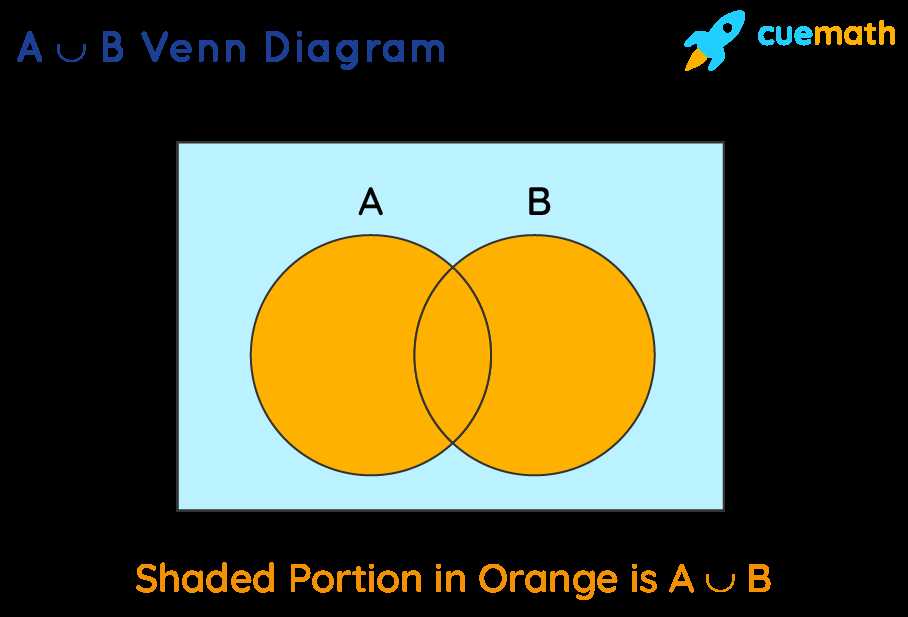
The A intersection B complement Venn diagram is a graphical representation that helps in understanding the relationship between two sets, A and B, and their complements. The diagram consists of two overlapping circles or ovals, each representing one set, with the intersection of the circles representing the elements that belong to both sets.
The A intersection B complement Venn diagram specifically focuses on the elements that belong to set A but not to set B. This is represented by the region outside the intersection, labeled as A ∩ B’, where A ∩ B’ denotes the intersection of A and the complement of B.
The diagram allows us to visually analyze and comprehend the relationship between the sets A and B and their complements. It helps in identifying the elements that are common to both sets, as well as the elements that belong exclusively to set A. By shading or labeling different regions of the diagram, we can clearly distinguish between these elements, allowing for easier analysis and interpretation.
Using the A intersection B complement Venn diagram, we can also determine the cardinality or number of elements in each region of the diagram. This information can be useful in various mathematical and logical computations, such as finding the probability of certain events or solving equations involving sets.
Overall, the A intersection B complement Venn diagram is a powerful tool for visualizing and understanding the relationship between two sets and their complements. It provides a clear representation of the elements that belong to set A but not to set B, allowing for easier analysis and interpretation of set operations and calculations.
Benefits of using the A intersection B complement Venn diagram
The A intersection B complement Venn diagram is a powerful tool that can provide several benefits in visualizing and understanding the relationships between two sets, A and B. This diagram helps to illustrate the elements that are common to both sets, while also highlighting the elements that are exclusive to each set, leading to a comprehensive analysis of the data.
One of the key advantages of using the A intersection B complement Venn diagram is its effectiveness in identifying shared and unique elements between sets. By visually representing the common elements in the overlapping region, it becomes easier to identify the similarities and differences between the sets. This allows for a better understanding and comparison of the two sets, which can be useful in various fields such as statistics, data analysis, and research.
The A intersection B complement Venn diagram also provides a clear visualization of the complement of set B within set A. This means that all the elements that are in set A but not in set B are represented outside the overlapping region. This can help in identifying the exclusive elements of set A, which can be essential in distinguishing between different categories or groups within a larger set of data.
Moreover, the A intersection B complement Venn diagram allows for easy interpretation and communication of complex concepts. By using visual elements such as circles or rectangles, it provides a concise representation of set relationships that can be understood by both experts and non-experts. This makes it a valuable tool in presenting data or findings to a wide audience, enhancing clarity and comprehension.
In conclusion, the A intersection B complement Venn diagram offers numerous benefits in analyzing data and understanding set relationships. Its ability to highlight common and exclusive elements, visualize complements, and facilitate interpretation make it a versatile tool in various fields. Whether used in academic research, business analysis, or everyday situations, this diagram can greatly assist in organizing and communicating complex information in a clear and concise manner.
Practical applications of the A intersection B complement Venn diagram
The A intersection B complement Venn diagram is a useful tool in various practical scenarios where the comparison of two sets is required. Here are a few practical applications of this diagram:
Marketing and Customer Analysis

In the field of marketing, the A intersection B complement Venn diagram can be used to analyze customer behavior and preferences. By representing Set A as existing customers and Set B as customers who have made a specific purchase, the intersection A intersection B complement represents existing customers who have not made that specific purchase. This information can be valuable for businesses to tailor their marketing strategies and target specific subsets of customers with personalized campaigns.
Crime Investigation
In crime investigation, the A intersection B complement Venn diagram can help identify potential suspects. Set A can represent individuals with a specific characteristic or involvement in a crime, while Set B can represent individuals who do not have an alibi or have other suspicious factors. The intersection A intersection B complement would then represent individuals who have the specific characteristic or involvement but do not have the suspicious factors, making them potential suspects for further investigation.
Healthcare and Medical Research
In healthcare and medical research, the A intersection B complement Venn diagram can be useful for analyzing patient data and identifying specific subsets of patients for further analysis. For example, Set A can represent patients with a certain genetic mutation, Set B can represent patients who have responded positively to a particular treatment, and the intersection A intersection B complement could represent patients with the genetic mutation but have not responded to the treatment. This information can help researchers identify potential factors affecting treatment efficacy and tailor personalized treatments for patients.
In conclusion, the A intersection B complement Venn diagram has practical applications in various fields such as marketing, crime investigation, healthcare, and medical research. By representing sets and their intersections, this diagram provides valuable insights and aids in decision-making processes.
How to Create an A Intersection B Complement Venn Diagram
A Venn diagram is a visualization tool that represents the relationships between different sets or groups of data. It consists of overlapping circles or shapes, with each circle representing a set and the overlapping areas representing the intersections between sets. In this article, we will discuss how to create an A intersection B complement Venn diagram.
Step 1: Identify the Sets
The first step in creating an A intersection B complement Venn diagram is to identify the sets you want to represent. In this case, we have two sets: set A and set B.
Step 2: Draw the Circles
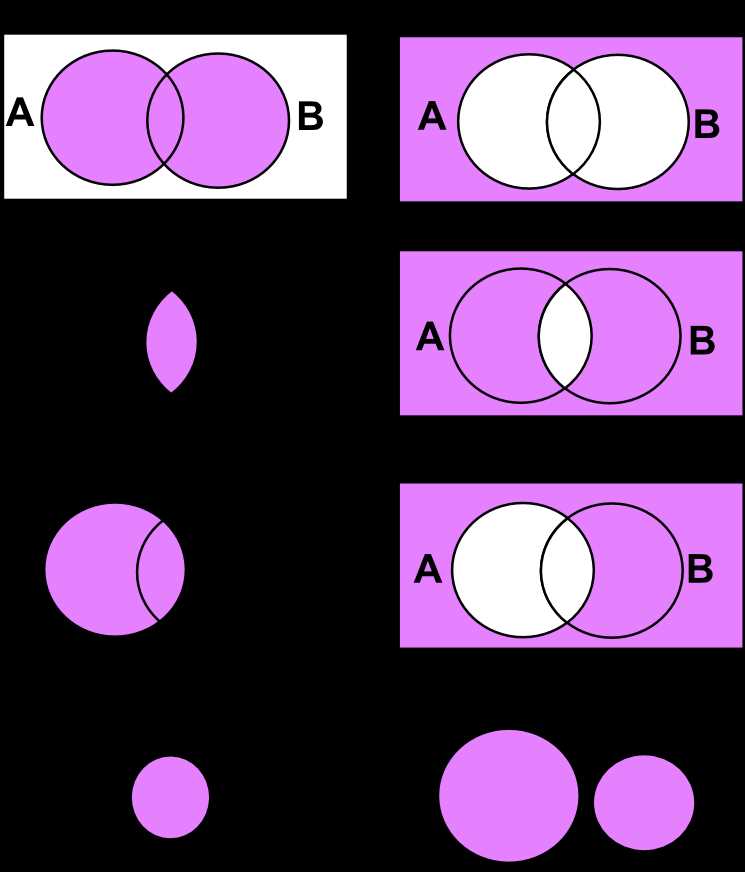
Next, draw two circles or shapes to represent set A and set B. Make sure the circles overlap to show the potential intersections between the sets.
Step 3: Label the Circles
Label each circle with the corresponding set name, i.e., “A” and “B”. This will help you differentiate between the two sets.
Step 4: Determine the Intersection
Identify the intersection between set A and set B, which represents the elements that are common to both sets. This area should be shaded or filled in to highlight the intersection.
Step 5: Find the Complement
To create an A intersection B complement Venn diagram, you need to find the complement of the intersection. The complement of a set represents all the elements that are not part of that set. In this case, it means finding the elements that are not in the intersection of set A and set B. This area should also be shaded or filled in to show the complement.
Step 6: Label the Intersection and Complement
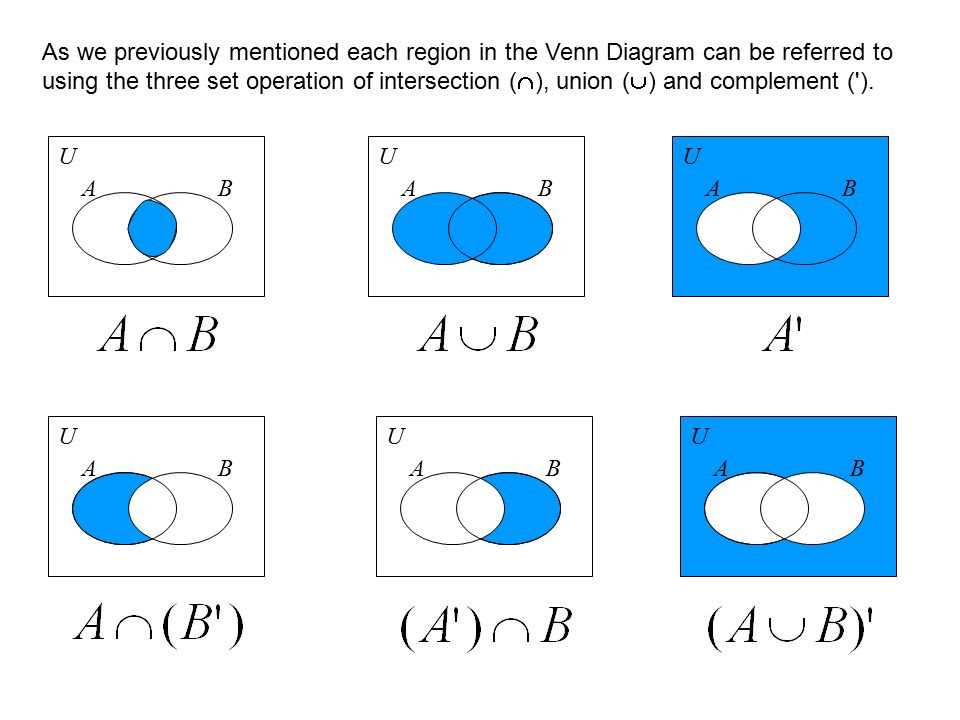
Label the shaded areas to clearly indicate which part represents the intersection of set A and set B, and which part represents the complement of that intersection.
Step 7: Add Additional Labels or Information
If desired, you can add additional labels or information to further clarify the Venn diagram. This could include specific elements or characteristics that belong to each set, or any other relevant details.
Creating an A intersection B complement Venn diagram can help you visualize the relationships between two sets and understand the elements that belong to the intersection and complement of those sets. It is a useful tool in various fields, including mathematics, statistics, and data analysis.