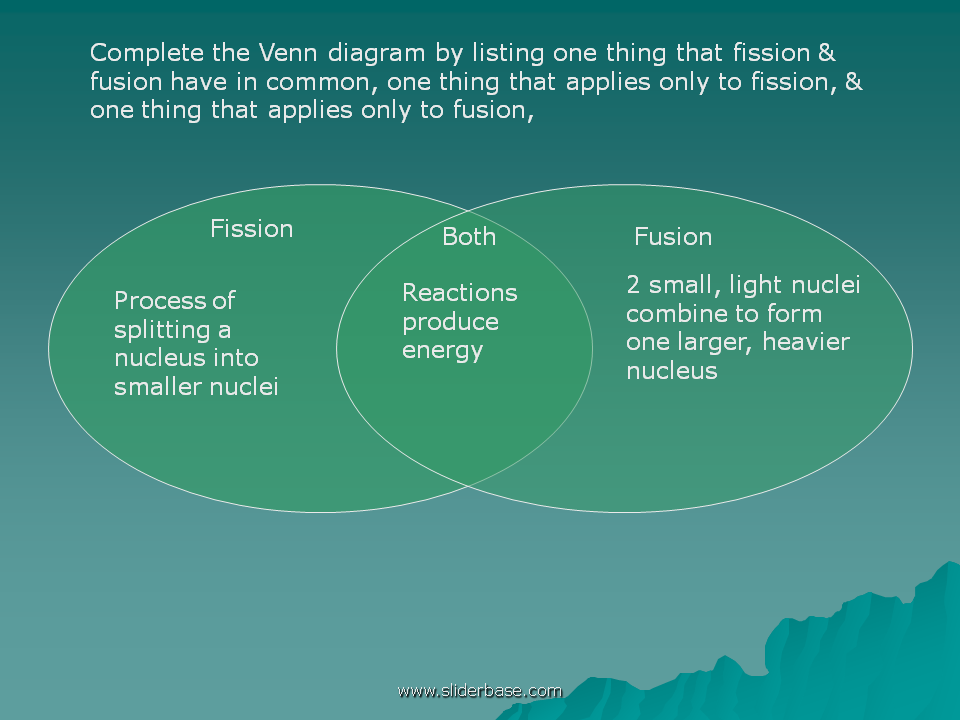
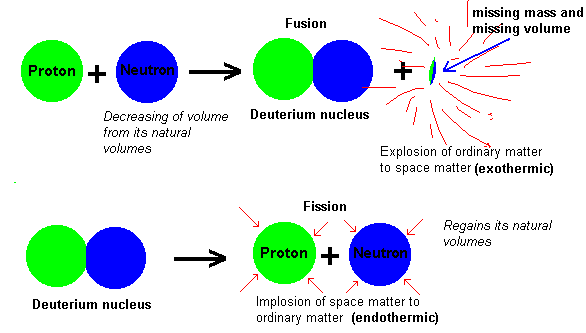
A Venn Diagram showing Fission vs Fusion. You can edit this Venn Diagram using Creately diagramming tool and include in your report/presentation/website.
Comparing and Contrasting Nuclear energy (Fission and Fusion). Fusion & Fission.
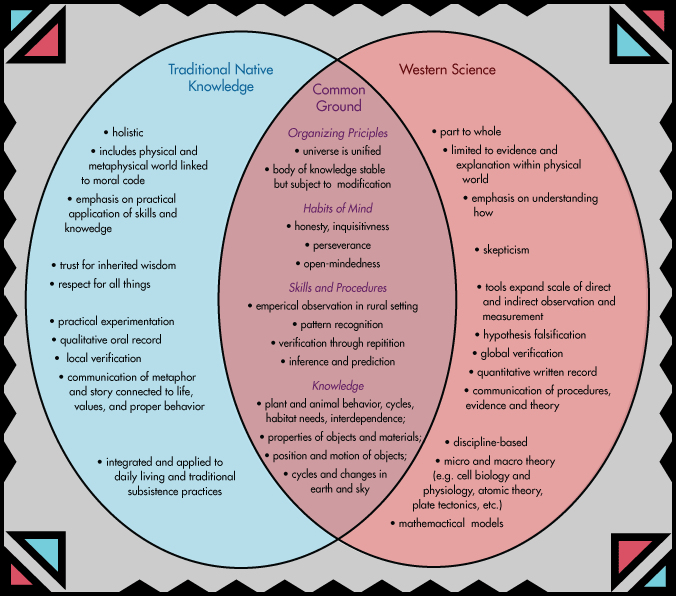
Venn Diagram. Can Nuclear Waste Be Recycled?
Digital image. Mother Nature Network.
N.p., n.d. Web.
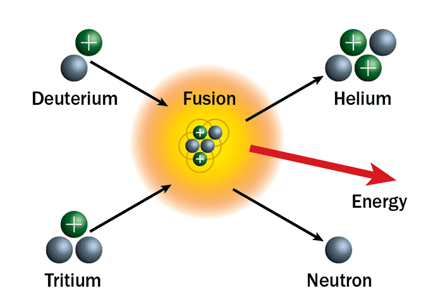
3 June The Sun gives off so much energy which explains the heat back on Earth. Fusion. Fission is when a atom splits emitting large amounts of.
A starter/revision activity venn diagram looking at fission and fusion.Most Common Text: Click on the icon to return to schematron.org and to enjoy and benefit. the of and to a in that is was he for it with as his on be at by i this had not are but from or have an they which one you were all her she there would their we him been has when who will no more if out so up said what its about than into them can only other time new some could these two may first then do.
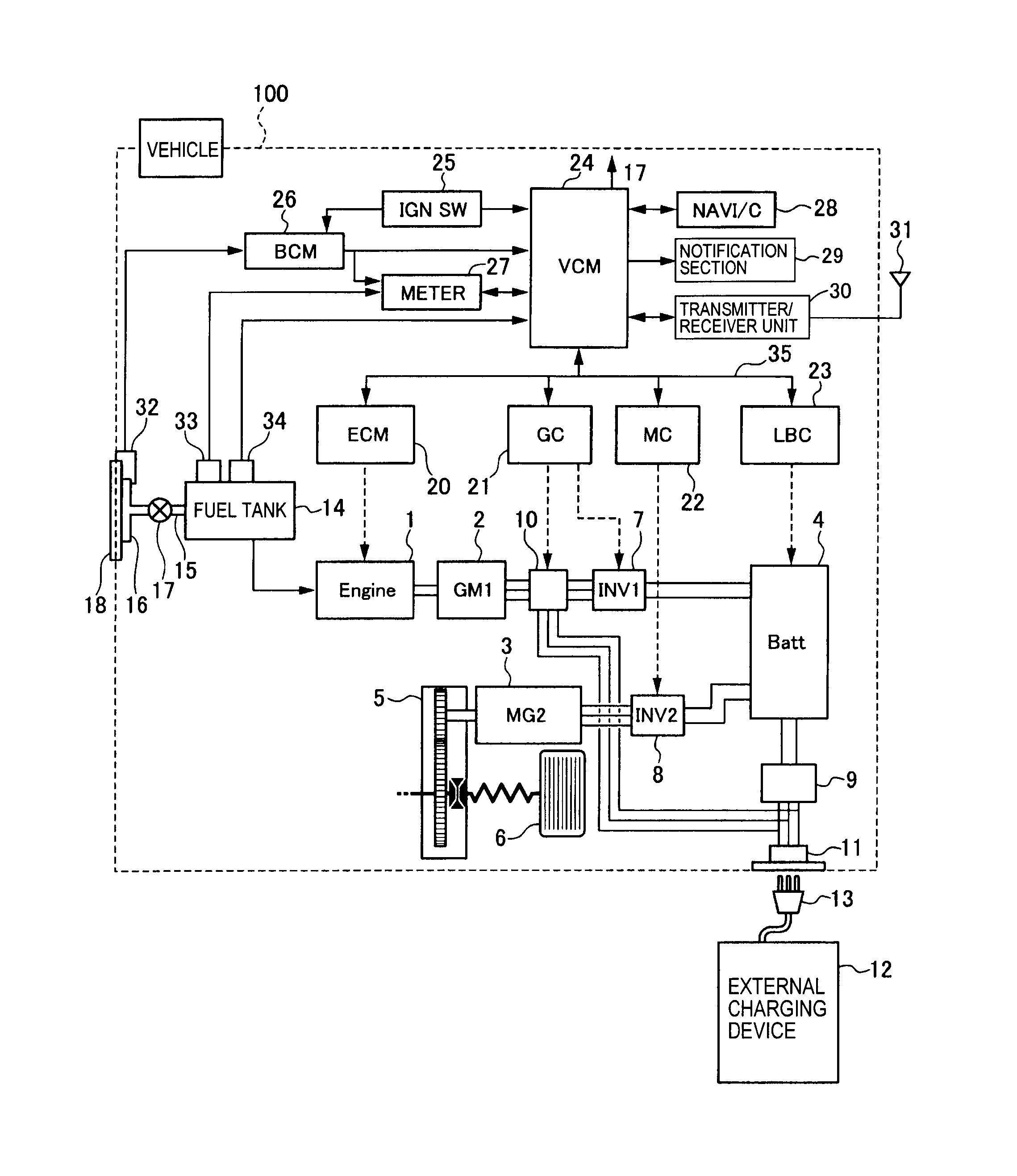
In the section Ship Design Analysis we will examine what spacecraft warships will need, what they won’t need, and what sort of tasks they will likely be required to perform. In the section Ship Types we will examine the thorny issue of the terminiology of the various types of spacecraft.
Search the world’s information, including webpages, images, videos and more. Google has many special features to help you find exactly what you’re looking for.
Oct 03, · I. Some of the best pushback I got on my election post yesterday was from people who thought Trump was a safer choice than Clinton because of the former’s isolationism and the latter’s interventionism. Since I glossed over that point yesterday, I want to explain why I don’t agree.
Trump has earned a reputation as an isolationist by criticizing the Iraq War. A quantum vacuum thruster (QVT or Q-thruster) is a theoretical system that uses the same principles and equations of motion that a conventional plasma thruster would use, namely magnetohydrodynamics (MHD), to make predictions about the behavior of the propellant. However, rather than using a conventional plasma as a propellant, a QVT uses the quantum vacuum fluctuations of the zero-point .Fission vs.
Fusion Venn Diagram by Kenneth Ditmore on PreziHe Kept Us Out Of War? | Slate Star Codex