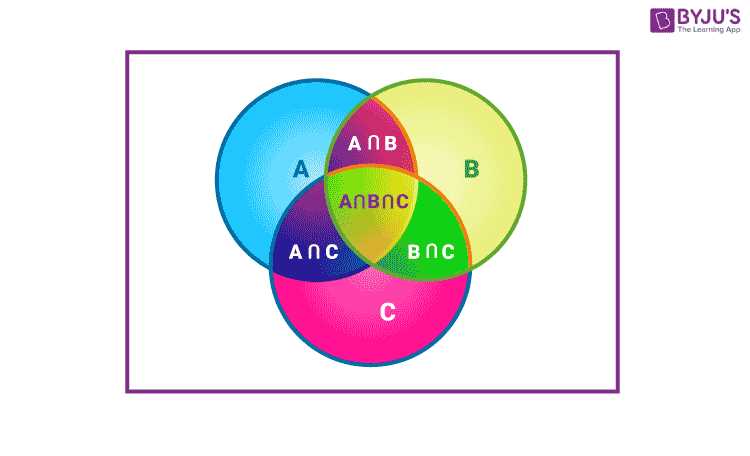
A Venn diagram is a graphical representation that depicts the relationships between different sets of data. It consists of overlapping circles or ellipses, where each circle represents a set, and the overlapping regions represent the intersection between sets. Venn diagrams are widely used in various fields, including mathematics, statistics, computer science, and logic, as they provide a visual way to understand the relationships between sets and their elements.
Calculating various aspects of Venn diagrams can be useful in many situations. One common calculation involves determining the size of the overlapping regions, which represents the intersection between sets. This can be done by counting the number of elements that belong to both sets, using set operations such as intersection, union, and complement. Another calculation involves finding the size of the union of two or more sets, which represents the total number of distinct elements in all sets combined.
In addition to size calculations, Venn diagrams can also be used to calculate probabilities. For example, given the sizes of different sets and the size of the overall sample space, one can calculate the probability of an event occurring by dividing the size of the event set by the size of the sample space. This can be particularly useful in probability and statistics, where Venn diagrams can visually illustrate the relationships between different events and their probabilities.
Overall, Venn diagram calculations provide a powerful tool for analyzing and understanding the relationships between sets of data. They can be used to determine the size of overlapping regions, calculate the size of unions, and even calculate probabilities. By visualizing these relationships, Venn diagrams help simplify complex data and make it easier to interpret and analyze. Whether you are a student, researcher, or professional, understanding and conducting Venn diagram calculations is an essential skill in many fields.
Understanding Venn diagrams
A Venn diagram is a visual representation of sets and their relationships. It is composed of overlapping circles, or sometimes other shapes, that represent different sets or groups. The overlapping regions of the circles show the elements that are common to both sets.
Venn diagrams are often used in mathematics, statistics, logic, and other fields to organize and analyze data. They can be used to compare and contrast different groups or categories, identify similarities and differences, and find intersections or unions.
Key components of a Venn diagram:
- Sets: Each circle represents a set or group of items. The items within each set share a common characteristic or property.
- Overlap: The overlapping portions of the circles show where the sets intersect, indicating the elements that belong to multiple sets.
- Regions: The non-overlapping areas of the circles represent elements that are unique to each set.
- Universal set: The space outside the circles represents the universal set, which includes all possible elements.
Using Venn diagrams:
Venn diagrams can be used for various purposes, such as:
- Comparing groups: Venn diagrams can help visualize the similarities and differences between different groups or categories.
- Identifying relationships: Venn diagrams can show the relationships between sets, such as subsets, unions, and intersections.
- Problem-solving: Venn diagrams can be used to solve logic puzzles or answer questions based on given information.
- Data analysis: Venn diagrams can be used to organize and analyze data, particularly in statistics and probability.
In conclusion, understanding Venn diagrams is essential for various fields where data organization and analysis are involved. These diagrams provide a clear visual representation of sets and their relationships, allowing for comparisons, identification of relationships, and problem-solving. By utilizing Venn diagrams effectively, it becomes easier to analyze data and make logical deductions.
Calculating elements in Venn diagrams

In Venn diagram calculations, it is important to understand how to calculate the number of elements in each section of the diagram. This can be done using various mathematical operations and formulas.
Intersection: The intersection of two sets refers to the elements that are present in both sets. To calculate the number of elements in the intersection, we can use the formula:
|A ∩ B| = |A| + |B| – |A ∪ B|
This formula takes into account the total number of elements in set A, the total number of elements in set B, and the number of elements that are present in both sets.
Union: The union of two sets refers to all the elements that are present in either set or both sets. To calculate the number of elements in the union, we can use the formula:
|A ∪ B| = |A| + |B| – |A ∩ B|
This formula takes into account the total number of elements in set A, the total number of elements in set B, and the number of elements that are present in both sets.
Complement: The complement of a set refers to all the elements that are not present in the set. To calculate the number of elements in the complement, we can subtract the number of elements in the set from the total number of elements in the universal set.
|A’| = |U| – |A|
By using these formulas and operations, we can effectively calculate the number of elements in each section of a Venn diagram and gain a better understanding of set relationships.
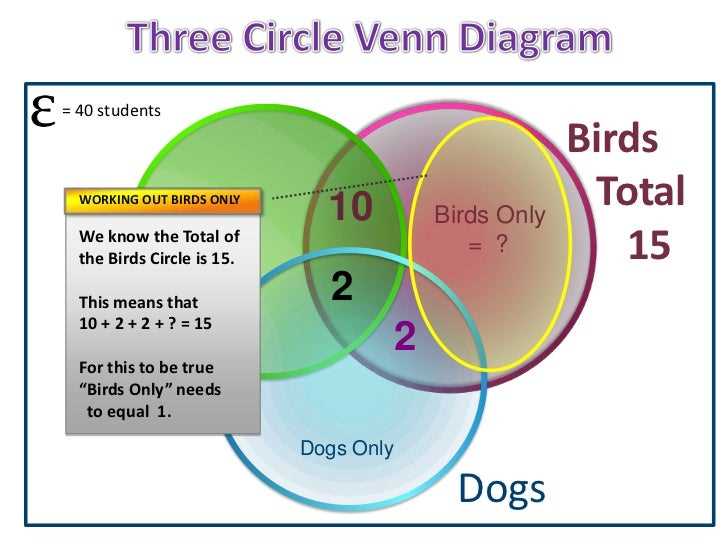
Calculating intersections of Venn diagrams
Venn diagrams are a useful tool for visualizing the relationships between different sets of elements. They consist of overlapping circles, with each circle representing a different set and the overlapping areas representing the intersection of those sets. Calculating the intersections of Venn diagrams allows us to determine the elements that are common to multiple sets and analyze their relationships.
To calculate the intersections of Venn diagrams, we need to consider the elements that are shared between the sets. This can be done by comparing the elements in each set and identifying the elements that are present in multiple sets. By determining the common elements, we can accurately represent the intersections in the Venn diagram.
One method of calculating the intersections is by using set notation. Each set can be represented by a list of elements, and the intersection can be determined by finding the elements that are present in all of the sets. The resulting set of elements represents the intersection.
Another approach to calculating the intersections of Venn diagrams is by using logical operators. By using AND or OR operators, we can combine the conditions of multiple sets and identify the elements that satisfy all of the conditions or satisfy at least one of the conditions. This allows us to determine the intersection or union of sets.
In conclusion, calculating the intersections of Venn diagrams involves analyzing the elements that are common to multiple sets. This can be done using set notation or logical operators. By determining the intersection, we gain insights into the relationships between different sets and can make informed conclusions based on the data presented in the Venn diagram.
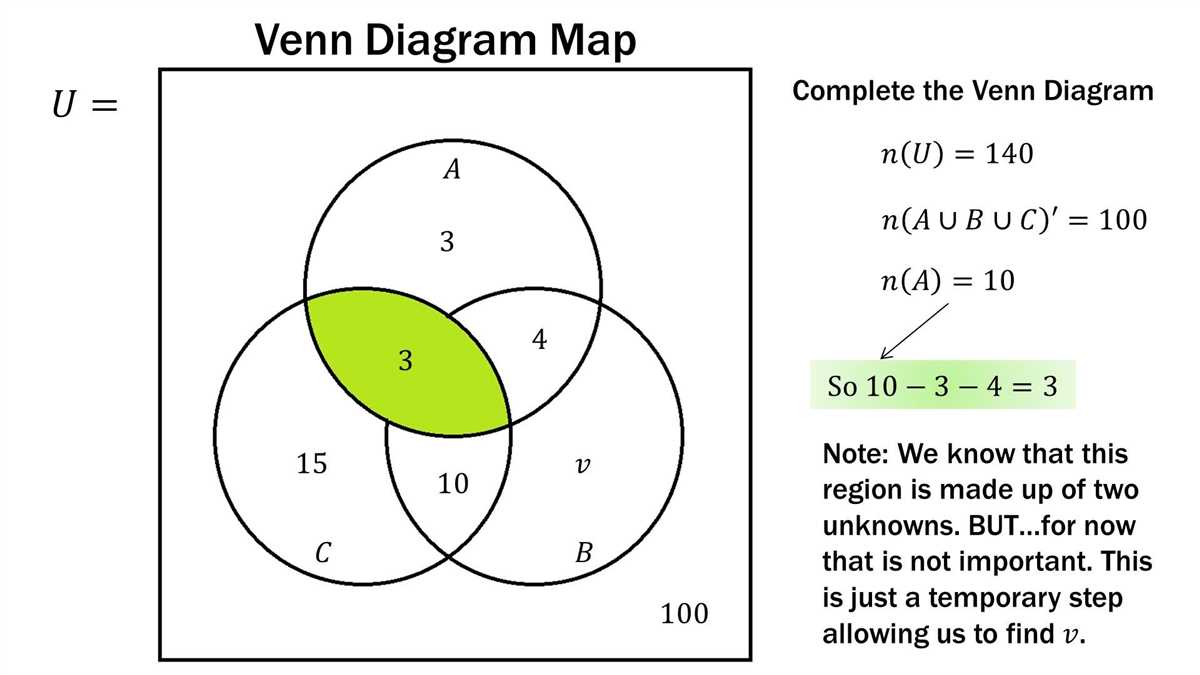
Calculating unions of Venn diagrams
When working with Venn diagrams, it is often necessary to calculate the union of multiple sets. The union of two or more sets is the set that contains all the elements present in any of the given sets. In terms of Venn diagrams, the union is represented by the overlapping region of the circles or curves.
To calculate the union of Venn diagrams, one should start by identifying the sets involved and the elements present in each set. Then, the union can be found by combining all the elements from each set without repetition. This can be done by creating a new set and adding the unique elements from each set to it.
For example, let’s consider a Venn diagram with three sets: A, B, and C. If A contains the elements {1, 2, 3}, B contains {2, 3, 4}, and C contains {3, 4, 5}, we can calculate the union of these sets by creating a new set and adding all the unique elements: {1, 2, 3, 4, 5}.
In some cases, the union of Venn diagrams may result in an empty set if there are no common elements among the sets. This means that the overlapping region of the circles or curves is empty, indicating that there are no elements that are present in all the given sets at the same time.
Overall, calculating unions of Venn diagrams involves identifying the sets and their elements, combining unique elements into a new set, and considering the possibility of an empty set when there are no common elements among the sets.
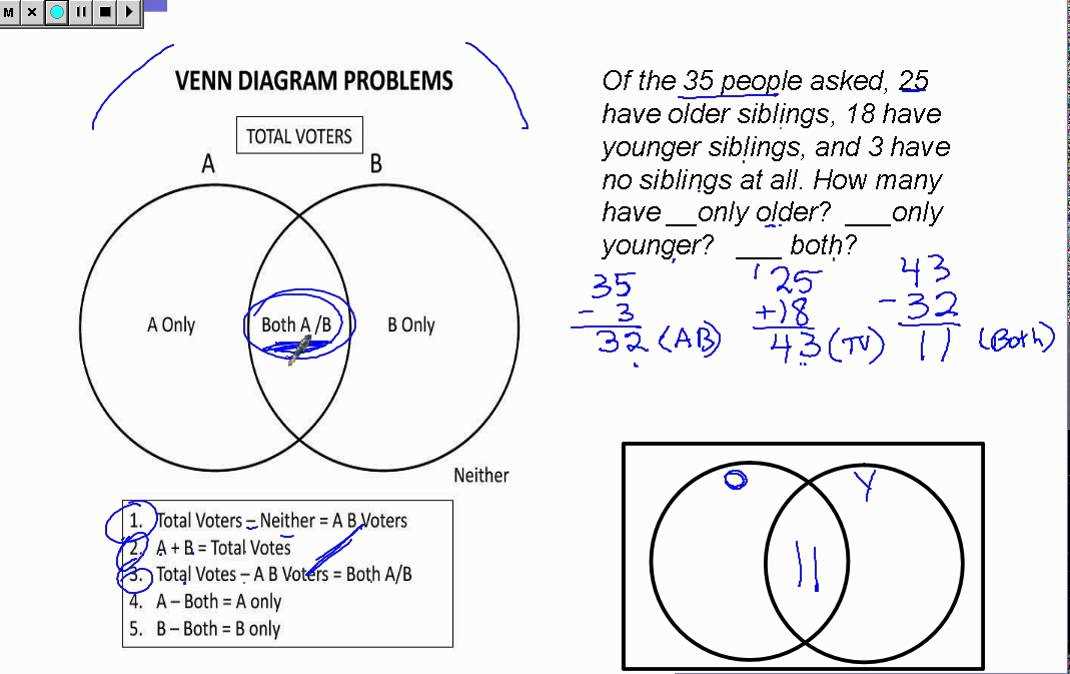
Calculating complements of Venn diagrams
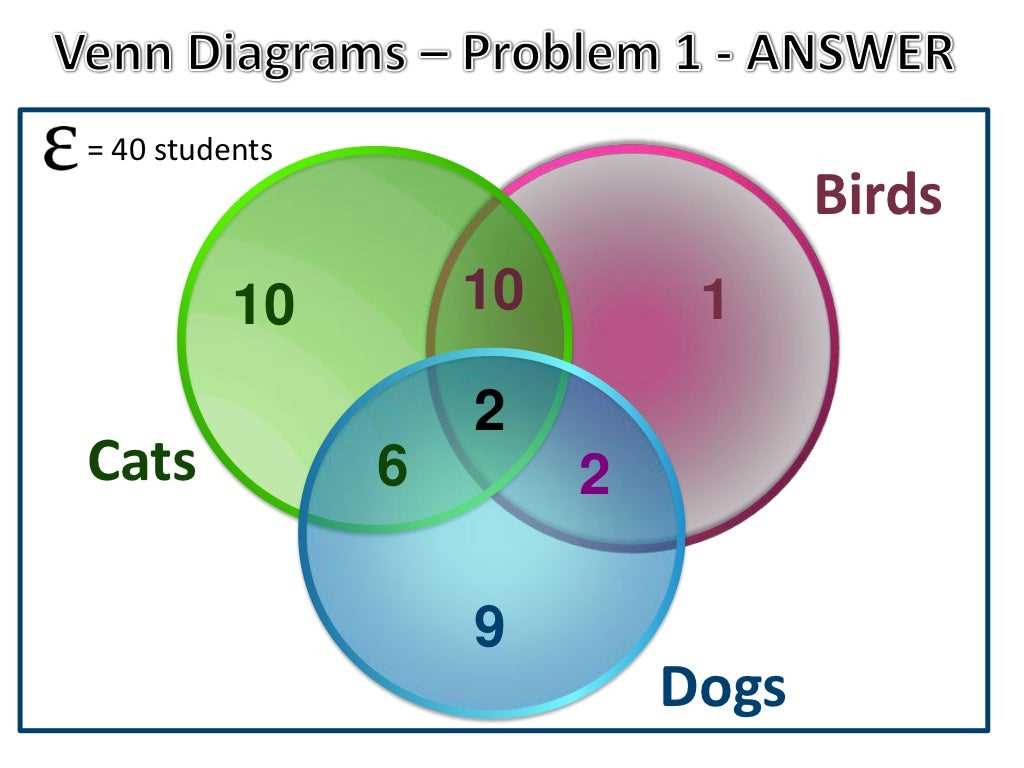
In Venn diagrams, the complement of a set refers to all the elements that are not in that set. Calculating complements can be useful in various applications, such as analyzing survey data or understanding overlapping categories. Here, we will explain how to calculate complements of Venn diagrams.
To calculate the complement of a set in a Venn diagram, you first need to determine the total number of elements in the universal set. The universal set represents all possible elements that could exist in the context of the Venn diagram. Once you know the total number of elements in the universal set, you can subtract the number of elements in the set you are calculating the complement for.
If you have a Venn diagram with two sets, A and B, and you want to calculate the complement of set A, you would follow these steps:
- Determine the total number of elements in the universal set.
- Count the number of elements in set A.
- Subtract the number of elements in set A from the total number of elements in the universal set.
For example, let’s say the universal set has 100 elements, and set A has 30 elements. The complement of set A would be 100 – 30, which is 70.
Calculating complements can become more complex when dealing with Venn diagrams with more than two sets. In such cases, you would need to consider the overlapping sections of the sets and determine the total number of elements in each section. By subtracting these values from the total number of elements in the universal set, you can calculate the complement of the desired set.
Overall, calculating complements of Venn diagrams allows us to understand the elements that do not belong to a particular set. By knowing how to calculate complements, we can gain deeper insights into the relationships and differences between sets.