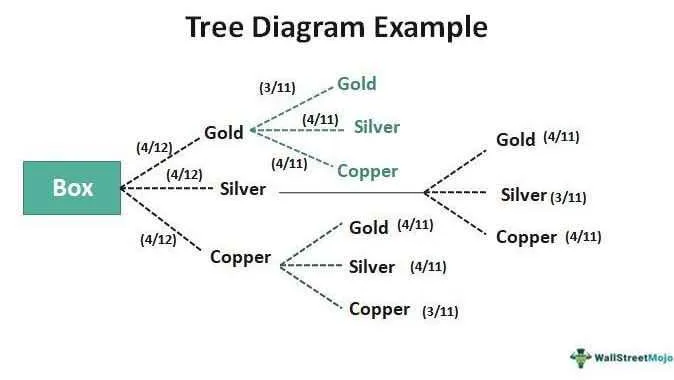
Choose software designed to simplify branching structures that represent all possible event results. Prioritize solutions offering intuitive interfaces with drag-and-drop functionality, enabling fast construction of multi-level scenario flows. Accurate labeling options for each node and edge ensure clarity in complex chains of consequences.
Look for features that support probability assignment or weighting at every junction, allowing precise calculation of final event chances. Export capabilities in multiple formats such as PDF, PNG, or SVG facilitate sharing and embedding in reports or presentations.
Efficiency in handling conditional outcomes is essential, especially for projects involving sequential decision processes or risk analysis. Tools with automatic updating of subsequent branches when altering initial assumptions reduce manual errors and speed up revisions.
Create Visual Models for Event Outcomes
To construct a clear model that represents possible event sequences, opt for tools that allow easy branching of options with corresponding likelihoods. Choose software or platforms that enable you to design a structure where each branch signifies a different potential result. These platforms typically let you assign probabilities to each outcome, ensuring you can visually track complex scenarios.
When selecting a tool, prioritize those offering drag-and-drop functionality, which allows rapid adjustments without needing extensive technical knowledge. This flexibility is key for users seeking efficiency in illustrating the relationship between multiple outcomes and their probabilities.
Another useful feature is the option to export your visual structure in various formats, such as PDFs or images. This ensures that your models can be easily shared and presented. Many advanced options also allow for conditional branching, where the next outcome is dependent on prior results, enhancing the depth of your representation.
For intricate models, seek out platforms with customizable styling options. Adjusting colors and labels can significantly enhance the readability and clarity of your model, making it easier to understand the interactions between different outcomes at a glance.
How to Construct a Probability Tree Diagram Step-by-Step
Begin by identifying all possible outcomes of the event or experiment. For each scenario, consider every subsequent possibility that can arise, and make sure to include all of them.
For each primary outcome, draw a line branching from the starting point. Label each branch with the associated likelihood or chance of that outcome. The number should be a fraction or decimal between 0 and 1, representing the probability of the event occurring.
Once the first set of branches is established, continue drawing additional branches from each outcome to reflect subsequent events. Ensure that each new line represents a different possibility, with corresponding chances at the end of each one.
Next, check that the sum of probabilities at each level of branching adds up to 1. This ensures that all potential outcomes are accounted for.
For more complex scenarios, extend the diagram by continuing to split each outcome into smaller possibilities. Each layer represents a different stage of the experiment or situation. Ensure that all possible combinations are captured at every step.
Finally, use this model to calculate compound outcomes. Multiply the probabilities along the branches to find the chance of a sequence of events. For instance, if you’re looking at two events, multiply their individual probabilities to determine the combined probability of both events occurring in sequence.
Be meticulous with your branching to avoid omitting any possibilities. Double-check your calculations and adjust if necessary.
Tools and Software Options for Creating Visual Decision Models
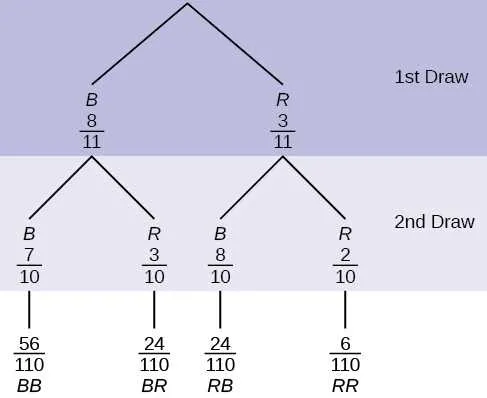
For constructing detailed decision models, there are several powerful tools available, each offering unique features to simplify the process and enhance your results. Below are some top software solutions:
- Lucidchart – A cloud-based platform with intuitive drag-and-drop functionality. Ideal for quickly visualizing complex decision paths. It supports real-time collaboration, which makes it perfect for teams.
- Microsoft Visio – Known for its rich set of templates, Visio is widely used for structured modeling. With its professional-grade symbols, it allows for creating both simple and advanced decision models.
- SmartDraw – Offers an easy-to-use interface and a wide variety of pre-built templates. Best suited for users who need to generate clear, concise models with minimal effort.
- Draw.io (diagrams.net) – A free, open-source tool with robust features. It can be used for creating a wide range of models, and it integrates seamlessly with Google Drive for storage and sharing.
- Creately – Provides a web-based platform with specific templates for decision analysis. Known for its collaborative features and support for both basic and advanced modeling.
For advanced customization and flexibility, consider using coding libraries like:
- Graphviz – A powerful open-source tool used for graph-based models. Requires some technical knowledge but provides complete control over design and styling.
- R (Diagramming Packages) – Useful for those familiar with R programming. Packages like “DiagrammeR” allow for the dynamic generation of models based on statistical data.
- Python (NetworkX) – A great option for those who prefer coding. NetworkX allows users to create and manipulate graph structures with Python, offering flexibility for advanced analysis.
For simpler tasks or casual use, online tools like Canva also provide basic templates to create quick, effective decision models with minimal learning curve.
Interpreting Outcomes and Calculating Likelihoods from Decision Maps
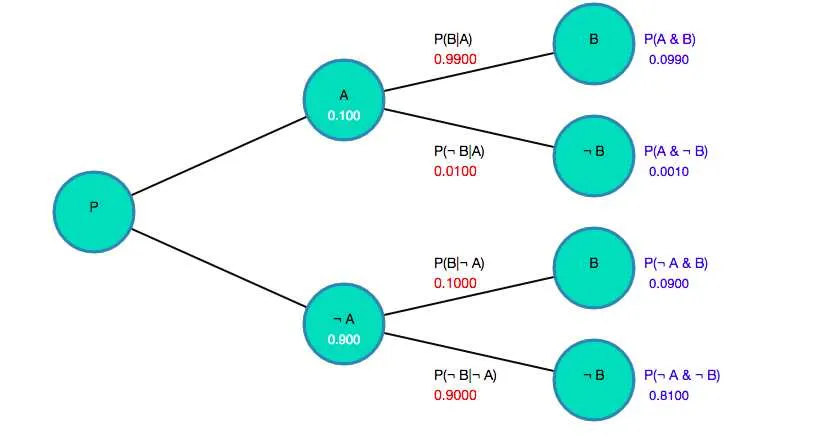
To determine the likelihood of a specific event occurring, begin by following each possible path from the starting point to the end. Each branch represents a potential outcome, and the number next to it indicates the chance of that outcome happening. Multiply the probabilities along a path to find the overall likelihood of that sequence. For instance, if one event has a chance of 1/2 and another follows with a 1/3 chance, the total likelihood for that path is 1/6.
When dealing with multiple branches, calculate the probability of each combination of events by multiplying the probabilities for each individual step along the route. The sum of these products gives the total likelihood for a particular outcome.
For conditional events, the likelihood of an outcome changes based on prior results. For example, if an initial event occurs, the probability for the following events will be conditional on that result. In such cases, adjust the probabilities accordingly to reflect the new conditions.
In situations where events are independent, the total likelihood of all outcomes can be found by multiplying the probabilities of individual events. However, for dependent events, you must adjust the calculation method to account for the relationship between events.
To analyze multiple potential results, sum the probabilities of all distinct paths leading to a common outcome. This provides a complete overview of the likelihood of that specific result occurring in a sequence of events.