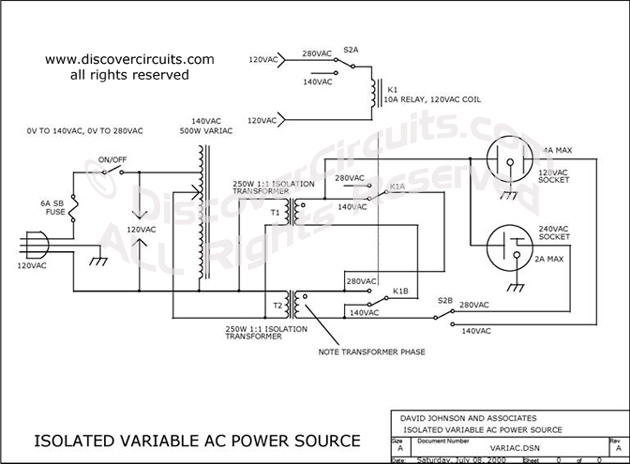
A variable voltage autotransformer (also known as variac) is a transformer which is able to transform Variable Voltage Autotransformer Wiring Diagram, Image.
A POWERSTAT Variable Transformer is a precision product packed with care. encountered while drilling holes, installing wiring, etc, during installation.
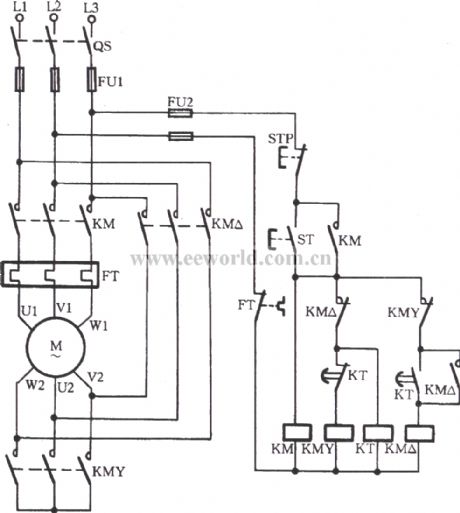
. in the tables and diagrams are for motor driven units and units with the knob. Transformers change the voltage by a change in the ratio of wire turns on the primary to Typical wiring diagram for buck-boost use of Variac.
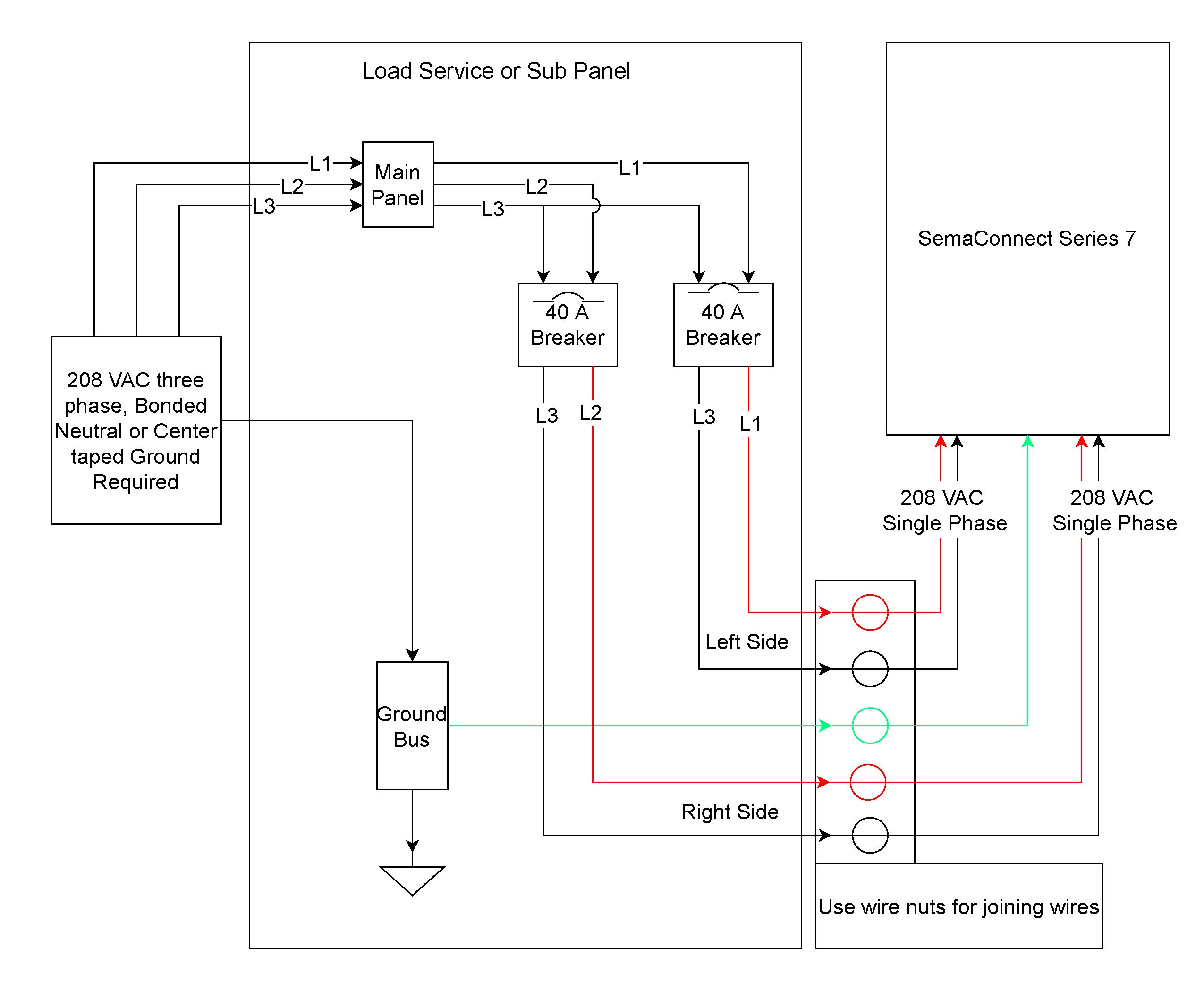
Schematics and Wiring Diagrams. General Wiring Information.
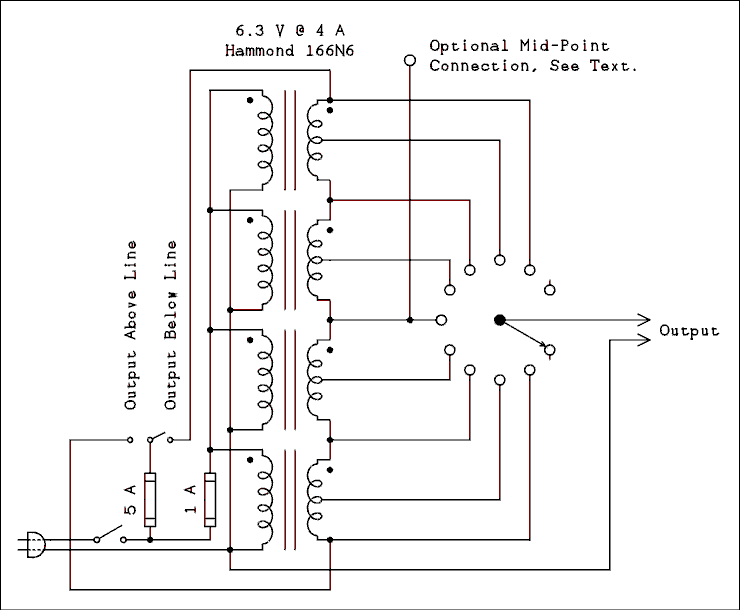
Common is used as the third leg in a three phase open delta or as neutral in a three wire single. Cooper wire is wound on a toroidal core by using high preci- METREL variable transformers provide an output voltage waveform cordance with diagram 1.supplementary transformer volt-ampere rating same as variac autotransformer load v maximum current 2 x variac rated current autotransformer z v secondary load v maximum current 17 x variac rated current supplementary transformer volt-ampere rating same as variac autotransformer figure 3. supplementary low-voltage transformer useful for.
VARIAC Variable Transformer Selector. Variac Variable Transformers include a full range of single an three phase models. Standard models include input voltages from VAC to VAC.
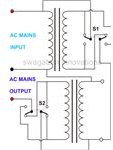
Frequencies to Hz can be accommodated on some versions. Special units for voltages to VAC and Amps are available.
Variac transformers are available that boost the output voltage in excess of twice the input voltage. Input frequencies to Hz can be accommodated on some models.
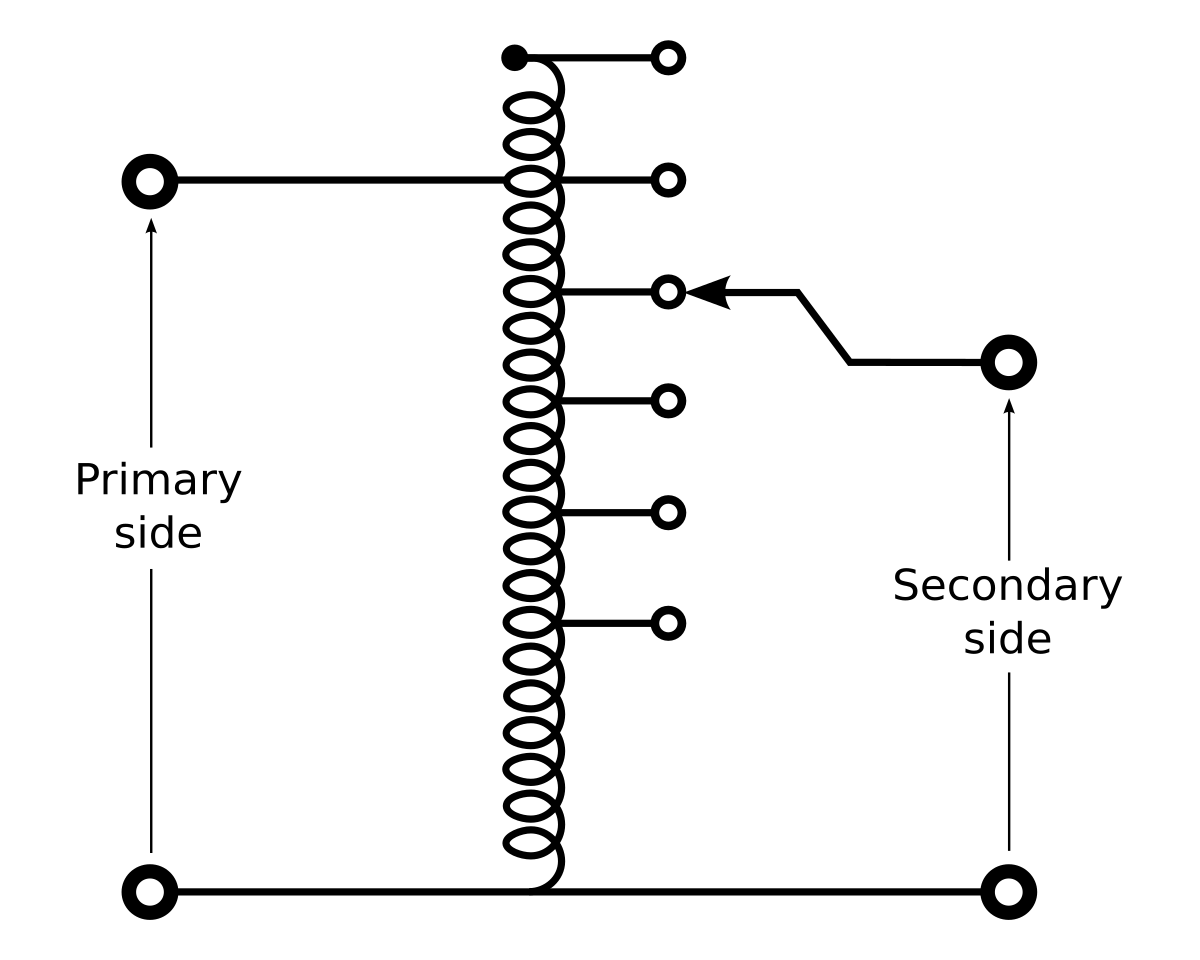
Variac Selector assists you in the selection of the best variable transformer for your application. An autotransformer has a single winding with two end terminals, and one or more terminals at intermediate tap points, or it is a transformer in which the primary and secondary coils have part of, or all of their turns in common. Dec 22, · It has a fried transformer with no markings and I am about certain it is 12V AC comming for the transformer, 2 yellow wires.
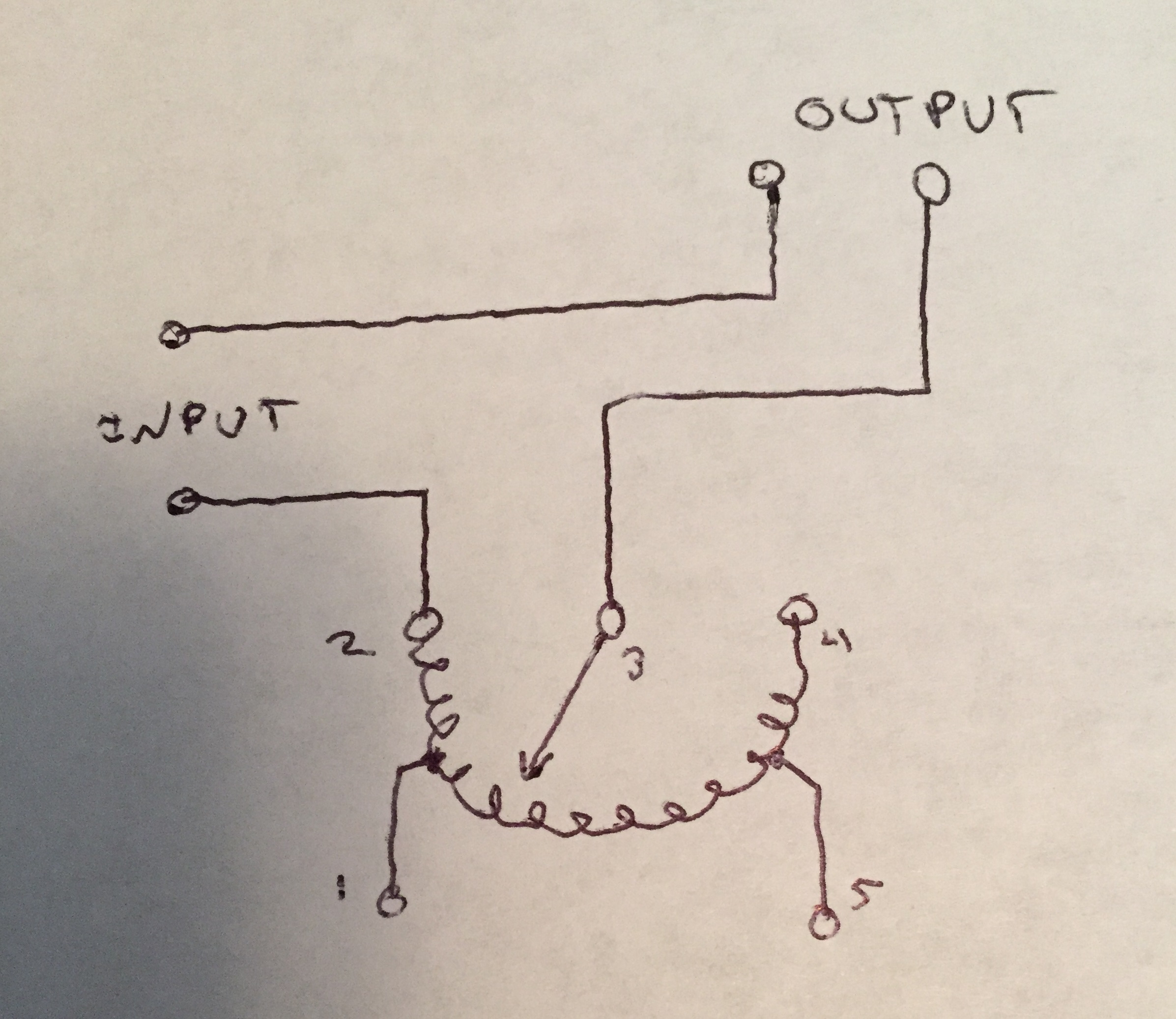
This variac has 5 connections for wires. There is like a schematic on the front just coil loops really.Village of the Banned – How do I wire a Variac?Variac? How to wire an use?